Adaptable Curricular Exercises (ACE) for Quantum Information Science (QIS)
Our goals for this site are to provide adaptable resources to support faculty, including those very new to these topics, who wish to add some student-centered, research-based QIS instruction to your classes.
We have materials for two different audiences, depending on the type of course you teach.
QM Course: Are you teaching quantum mechanics in a physics department to (mostly) majors, and want to add a short unit on quantum information (e.g. quantum computing or cryptography) within your course?

QIS Course: Are you teaching a quantum computing/QIS course to a diverse population of students (e.g. computer science, physics, engineering, math...), and want to support students in the basic quantum mechanics needed?
(These materials are under development)
And: if you teach undergraduate quantum mechanics to physics students and are looking for a suite of student-centered materials to help you with the entire QM course, please visit our Adaptable curricular materials for Quantum Mechanics site.
Tools for introducing QIS in a QM course
Who is this for? An instructor teaching Quantum Mechanics who would like to add some quantum information science topics to their physics course.
(Materials are suitable for faculty new to these topics.)
Topics: We have divided our materials into three main topical areas.
Each is standalone - materials can be taught without any prerequisite material from the other groups.
(Because of this, there are some duplicate materials across the groups.)
We do not intend for the materials to be used wholly as written. Rather, they form a complete set that a faculty member can pick and choose from as it fits their schedule, the material already taught, and the interests of both the faculty member and student.
Types of instructional materials
The “instructional materials” found on this site include: lecture notes for faculty, concept tests, homework questions, online tutorials, and assessments.
Please use and adapt whatever is helpful to you, however it will most benefit your students. Please credit our work if you share your materials beyond your own classes. Please make an effort to keep assessment materials off the open web - alter questions for your students.
 Example Classroom Implementations
Example Classroom Implementations
Curriculum designers Dr. Steven Pollock and Dr. Gina Passante have each taught this material in their classes. Feel free to download our lecture notes - we are happy for you to use whatever material works for your class.
Please email if you try our materials and have any feedback:
steven.pollock (at) colorado.edu or gpassante (at) fullerton.edu
Steven Pollock's CU Boulder Implementation
CUB is a research-intensive public institution. I teach these materials in junior or senior-level undergraduate quantum mechanics courses, which currently all follow a spins-first curriculum (using McIntyre's Quantum Mechanics textbook.)
Each sequence below takes me one week. These are all taught in "large lecture" (75+ student) settings with three 50-minute lectures/week.
- I teach entanglement and EPR midway through the first semester (this is largely following McIntyre's Chapter 4 treatment)
- I teach qubits and teleportation late in the second semester (senior-level) quantum course, as a basic introduction to quantum information science. (This is largely following McIntyre's Chapter 16 treatment)
Please reach out if you have questions or feedback: steven.pollock (at) colorado.edu
Gina Passante's CSUF Implementation
CSUF is a primarily undergraduate, large, Hispanic-serving institution. I teach these materials in several of my quantum mechanics courses at the undergraduate and master's levels.
- Qubits, Quantum Gates, and Teleportation: I choose to teach this in the middle of a first semester of undergraduate QM. My course is spins-first and I do a "quantum computing" week to apply what they have learned before moving to position wave functions.
- Entanglement and EPR: I teach an introduction to entanglement and a conversation of "spooky action at a distance" when I teach the "qubits, quantum gates, and teleportation" material. But the discussion about the EPR paradox and the Bell inequalities is taught at the master's level.
- Quantum Cryptography: This is a one-class supplement that can be taught at any level. The only prerequisite knowledge is superposition states, measurement, and bra-ket notation. The example here was done in my first-semester, junior-level quantum mechanics course.
Feel free to reach out if you have questions (gpassante at fullerton dot edu).
 Qubits, Quantum Gates, and Teleportation
Qubits, Quantum Gates, and Teleportation
In this module, we introduce quantum bits (called qubits), the elementary quantum gates that make up a quantum computer, leading up to an algorithm to teleport a quantum state from one location to another.
These materials are intended for a faculty member to select and adapt relevant pieces to use in their classroom.
In our courses, this topic takes 1 week to cover.
 Notes for Faculty
Notes for Faculty
We have written brief notes on the topics in this module that are intended for faculty adopters.
Browse below, or download all as a single pdf file (see Materials Download section below)
If computers that you build are quantum
then spies everywhere will all want ‘em.
Our codes will all fail
and they’ll read our email,
till we get crypto that’s quantum, and daunt ‘em
- Jennifer and Peter Shor
This first subunit involves a brief introduction to QIS: quantum information science. For physics majors, an introduction to the big ideas of quantum information and quantum computing serves to motivate the upcoming topics. Some discussion of the "hype" vs realities of QIS might be in order here. A little background in classical computers may be relevant (note that some are discussed in the "Parts of a computer" section below)
Classical computers store, process, and manipulate bits (characterized abstractly as 0 or 1). Current optimal algorithms for factoring large numbers take time that grows exponentially with the size of the number to be factored, and current commercial encryption takes advantage of that fact. If one were to have functioning quantum computers that could store and manipulate quantum bits (i.e., superpositions of 0 and 1 - which we will discuss shortly), there exists an algorithm (Shor's) that could "decrypt" current common protocols exponentially faster. This has generated excitement and hype, and there are major efforts in industry and academia to construct such machines and develop new algorithms. A key aspect of quantum computing is the concept of "basis size" - for a 4-bit quantum computer, a given stored qubit can be a superposition of up to $2^4 = 16$ basis states. In some sense, this represents exponentially more information in a single qubit than the 4 bits a classical computer stores.
The intent of adding QIS to a quantum class for physics students is to see how the tools we have learned (e.g. concepts of superposition and measurement) allow us to understand the basic language and ideas involved in a number of QIS applications, including quantum computing, cryptography, and teleportation. The goal is not a course in these topics, but a brief introduction to motivate further study.
Reference: "How Media Hype Affects our Physics Teaching: A Case Study on Quantum Computing", Meyer et al, TPT 61, 339 (2023) DOI: https://doi.org/10.1119/5.0117671
This is a (brief) introduction to qubits (including Dirac notation) and superposition. For students in a physics majors quantum class, this is intended to make the quick shift from more general quantum observables to 0's and 1's.
Bits in a computer (or, as we’ll refer to them, classical bits in a classical computer) are 0 or 1. The distinction between a bit and a quantum bit, or qubit, is that a qubit can be in 0, 1, or a superposition of 0 and 1.
If you measure a qubit, it can only have one of two different values: 0 or 1 (just like a classical bit). But before measurement, it can exist in a superposition of 0 and 1.
Mathematically, we write $ | 0 \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$ and $ | 1 \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}.$
These qubit states form a basis in the two-dimensional Hilbert space (complex vector space). A key difference between the discussion of measurement in quantum computing vs other areas of quantum mechanics is that we do not discuss observables but rather only talk about measuring a “0” or a “1”. In contrast, if we were talking about measuring the spin of an electron, I would talk about measuring the $S_x$ (or spin in the z-direction) and getting a value of $\pm \hbar/2 $. When building a quantum computer, it is important to discuss the physical system realizing the qubit and what observable is being measured, but for our theoretical discussion of quantum states, we will refer to it simply as measuring "0" or "1".
The basis created by $|0\rangle$ and $|1 \rangle$ is called the "computational basis" or the "standard basis".
The general state of a qubit can be written as $a|0\rangle + b|1\rangle$, where $a$ and $b$ are complex numbers (they are the probability amplitudes) and we require that $|a|^2 + |b|^2 = 1$ .
For this general qubit state, the probability of measuring a 0 is $|a|^2 $ and the probability of measuring a 1 is $ |b|^2 $.
Sample related online Tutorial:
https://acephysics.net/tutorials/introduction-to-quantum-gates/1-quantum-bits
The remainder of that Tutorial serves as a basic introduction to single-particle gates (see section on gates below)
Classical computers work with bits, denoted by states 0 or 1. The physical implementation of those bits is rather arbitrary (typically low and high voltage on a wire), but for many practical computing purposes also irrelevant. The same will be true for quantum computers, but now the qubit can be in any superposition state $a\ket{0} + b\ket{1}$.
Classical computing requires gates: operators that act on a bit (one or more) and output a resulting bit. The "Not" gate is the simplest single-bit gate: inputing a 0 yields a 1 and vice versa. This can also be thought of as a logic operation (interpret 0 = "false" and 1 = "true") The "And" gate acts on 2 inputs and returns a single output, the logical "And" operation.

Quantum gates similarly take input states, act on them, and produce output states. The final stage of a set of quantum operations will ultimately be a measurement, but the sequential operations should not make any measurements (indeed, avoiding such collapse of the quantum superposition state is a major engineering challenge at the moment). Schematically, the process can be thought of schematically like this:
Much current physics and engineering research is devoted to studying how to physical implement qubits - examples include spin-1/2 systems where 0 and 1 represent "up" and "down" spin in the Z direction, and certain gates could involve applied magnetic fields (for instance), but the states could also be photon polarization, energy levels of trapped atoms, current in Josephson junctions, or many more. For discussing gates and algorithms, just as with classical bits, this physical implementation is not essential.
A quantum gate is an operation performed on qubits. Mathematically, gates are associated with unitary and linear operators. Linear means e.g. $Z(a\ket{0} + b\ket{1}) = aZ\ket{0} + bZ\ket{1}$. Thus, one way to define them is by their operation on computational basis states.
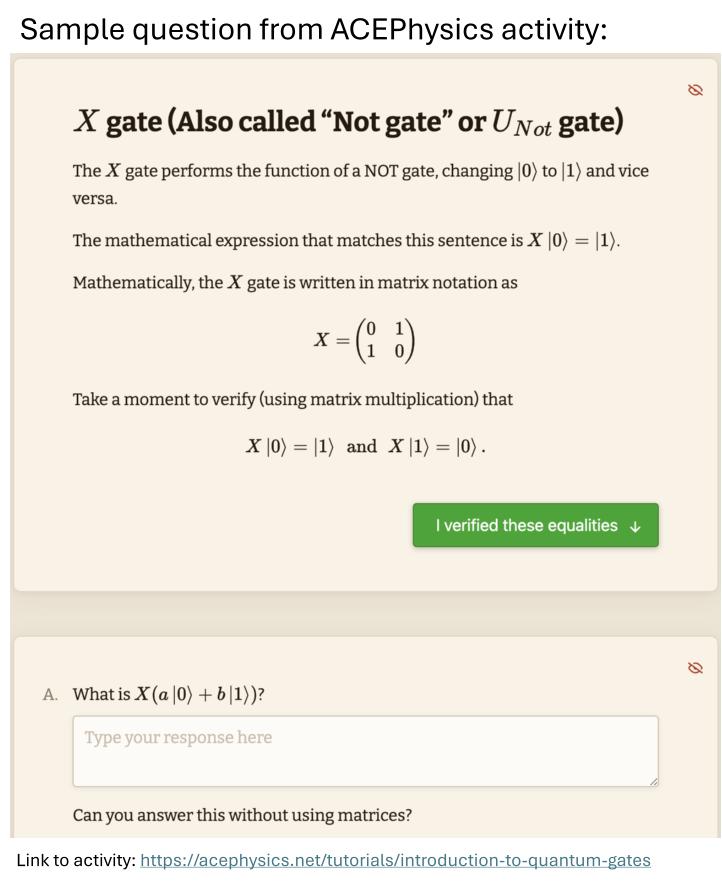
- $X$-gates: $X\ket{0} = \ket{1}, \ \ X\ket{1}=\ket{0}$.
(The $X$-gate is a 'bit flip' or NOT gate: taking $\ket{0}$ to $\ket{1}$, and vice versa. ) - $Z$-gates: $Z\ket{0} = \ket{0}, \ \ Z\ket{1}=-\ket{1}$.
The $Z$-gate is thus sometimes called a "phase gate" (flipping the phase of $\ket{1}$ states.) - $Y$-gates: $Y\ket{0} = -i \ket{1}, \ \ Y\ket{1}=i\ket{0}$.
The $Y$-gate is thus a combination of the previous two ($Y = iZX$). - Identity ($I$): $I\ket{0} = \ket{0}, \ \ I\ket{1}=\ket{1}$.
The identity operator $I$ does not alter input states in any way. - Hadamard gates:
$H \ket{0} = \frac{1}{\sqrt{2}} ( \ket{0} + \ket{1}) \;\; \text{ and } H\ket{1} = \frac{1}{\sqrt{2}} ( \ket{0} - \ket{1})$.
The Hadamard is a common and useful gate in quantum computing algorithms - it converts pure computational states into superposition states.
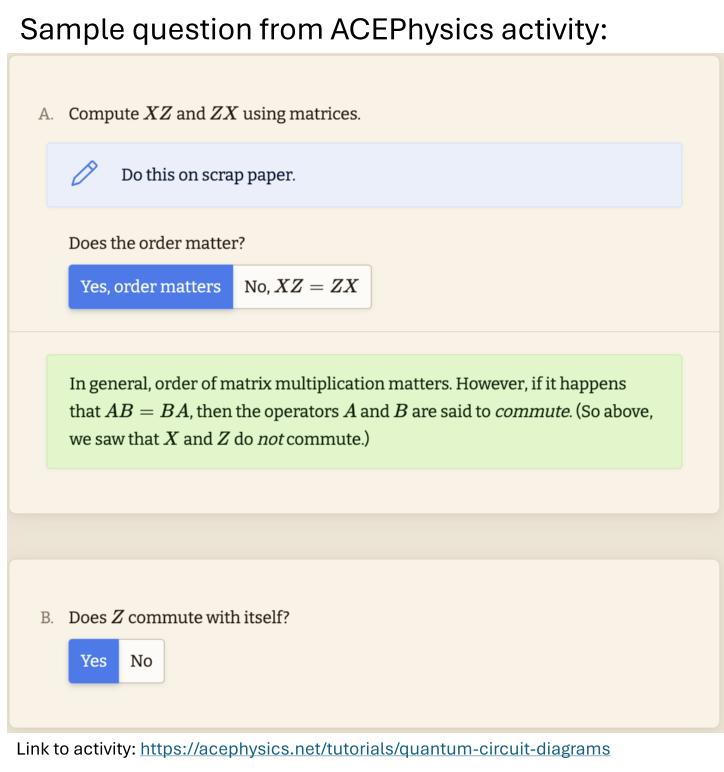
Note that $ XX = YY = ZZ = H H = I$, and that order matters, e.g. $X$ does not commute with $Z$.
So e.g. $a\ket{0} + b \ket{1} \doteq \begin{pmatrix} a \\ b \end{pmatrix}$ (with $\doteq$ read "is represented by")
In this representation, the most common gates are akin to the Pauli operators:
$ X\doteq \mqty(0 & 1 \\ 1 & 0), \;\; Y \doteq \mqty(0 & -i \\ i & 0), \;\; Z \doteq \mqty(1 & 0 \\ 0 & -1) \;\; \text{ and } I \doteq \mqty(1 & 0 \\ 0 & 1)$
The Hadamard gate is $H \doteq \frac{1}{\sqrt{2}}\mqty(1 & 1 \\ 1 & -1)$.
A natural follow-up is to ask the same question for $H\ket{0}$. Our students scored similarly to the previous one. These questions provide elementary practice and serve as conversation starters. $H$ plays a huge role in algorithms: often the first step is to start with a bunch of $\ket{0}$ states, then act $H$ on each to get a collection of superposition states.
Sample related online Tutorial:
An online introduction/tutorial on quantum gates is available on acephysics.net:
https://acephysics.net/tutorials/introduction-to-quantum-gates/1-quantum-bits
Circuit diagrams use lines to indicate individual qubits and boxes to indicate quantum gates. They are read from left to right. The following diagram depicts the equation: $\ket{\psi}_{out} = X Z \ket{\psi_{out}}$.
![]()
Note how the equation looks "backwards" compared to the circuit, but it is clear in both that the $Z$ gate acts first. We can also depict a measurement by using a symbol of a "meter" as shown below (note that different textbooks often have different conventions for a measurement symbol).
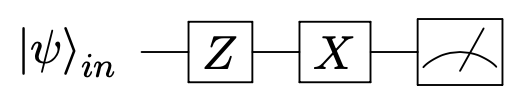
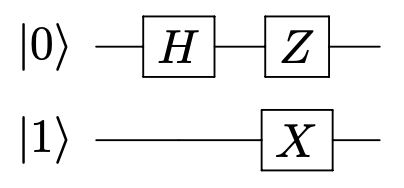
When we add additional qubits, they are shown as additional lines where the top line is understood to be the first qubit. The circuit diagram below shows the output for the first qubit is $ZH\ket{0}$ and the output of the second qubit is $X\ket{1}$.
Sample related online Tutorial:
A very brief online introduction to quantum circuits is available on acephysics.net:
https://acephysics.net/tutorials/quantum-circuit-diagrams
When moving to N-qubit systems, the dimensionality of your basis grows as $2^N$. Here we briefly introduce students to the ideas of combining two single particle states into a larger-dimensional 2-qubit state, and how to represent this in Dirac (or matrix) notation, using the language of tensor products.
There is only so much that can be done with a single qubit. To add a second qubit, we use the tensor product $\otimes$. If the first qubit is in the state $\ket{0}$ and the second qubit is in the state $\ket{1}$, then the two-qubit state can be written as $\ket{0} \otimes \ket{1}$. There are several shorthand ways to write this. Below are all equivalent formulations:
$ \ket{0} \otimes \ket{1} = \ket{0} \ket{1} = \ket{01}$
For brevity, the last one is most commonly used unless it is important to emphasize the states of the individual qubits, in which case the $\otimes$ symbol will be used.
When dealing with 2-particle systems, 2-qubit operations can (sometimes) be described as a tensor product of operators (e.g., $\hat{A}\otimes\hat{B}$), and can (always) be represented by a 4x4 matrix in the 4-d two-qubit Hilbert space.
For example, in the circuit below, the first set of gates can be written as a tensor product: $H \otimes Z$, but based on the information we have, the second gate $U$ cannot be broken down into a separate gate on each qubit.
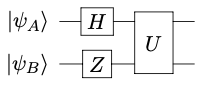
Mathematically, the circuit is represented as:
$ U(H\otimes Z) (\ket{\psi_A} \otimes \ket{\psi_B}) = U ( H\ket{\psi_A} \otimes Z\ket{\psi_B})$
(By convention, the ordering of the basis states, $\ket{00}, \ket{01}, \ket{10}, \ket{11}$ are counting up in binary)
The tensor product $\ket{\psi_1} \otimes \ket{\psi_2} = (a \ket{0} + b\ket{1}) \otimes (c \ket{0} + d\ket{1}) = ac \ket{00} + ad\ket{01} + bc \ket{10} + bd\ket{01}$.
In matrix notation, $\ket{\psi_1} \otimes \ket{\psi_2} \doteq \begin{pmatrix} a \\ b \end{pmatrix} \otimes \begin{pmatrix} c\\d\end{pmatrix} =\begin{pmatrix} ac\\ ad\\ bc\\ bd \end{pmatrix}$
This can be summarized by a simple computational trick:
$\begin{pmatrix} a \\ b \end{pmatrix} \otimes \begin{pmatrix} c\\d\end{pmatrix} =\begin{pmatrix} a\begin{pmatrix}c\\d \end{pmatrix} \\ b \begin{pmatrix}c\\d \end{pmatrix} \end{pmatrix} = \begin{pmatrix} ac\\ ad\\ bc\\ bd \end{pmatrix}$
$= \begin{pmatrix} a_{11}b_{11} & a_{11}b_{12} &a_{12}b_{11} &a_{12}b_{12} \\ a_{11}b_{21} & a_{11}b_{22} &a_{12}b_{21} &a_{12}b_{22}\\ a_{21}b_{11} & a_{21}b_{12} &a_{22}b_{11} &a_{22}b_{12}\\ a_{21}b_{21} & a_{21}b_{22} &a_{22}b_{21} &a_{22}b_{22} \end{pmatrix}$
Sample related online Tutorial: Tensor Products -
An online introduction/tutorial on tensor products is available on acephysics.net:
https://acephysics.net/tutorials/tensor-products
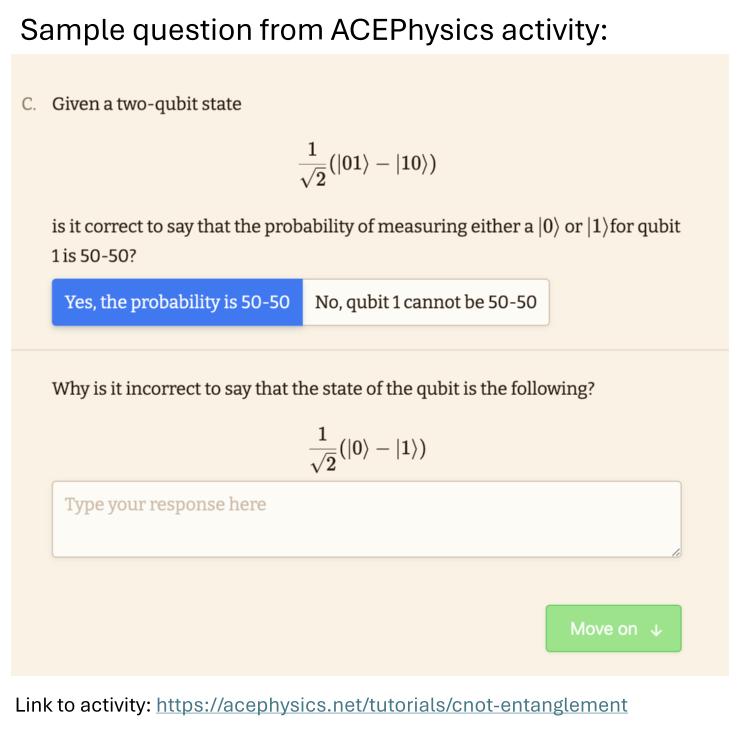
Two (or more) particle quantum systems can exhibit interesting correlations (entanglement) stronger than any classical system.
A state is entangled when it cannot be written as a single tensor product of two single-qubit states.
For example, consider the state $\tfrac{1}{\sqrt{2}}(\ket{00} + \ket{01})$. This state is NOT entangled, because we can 'factor' it into $\ket{0} \otimes \tfrac{1}{\sqrt{2}}(\ket{0} + \ket{1})$. In this case the first qubit is in the state $\ket{0}$ and the second state is in the state $\tfrac{1}{\sqrt{2}}(\ket{0} + \ket{1})$.
In contract, we can look at the entangled state $\tfrac{1}{\sqrt{2}}(\ket{00} + \ket{11})$. There is no way to write a ket for the first or second qubit on their own. The state must be written together.
Note: It is possible to describe the first qubit using a reduced density operator. The state of the first qubit would be the completely mixed state $\rho_1 = \frac{1}{2}\mqty( 1 & 0 \\ 0 & 1)$.
Second note: Entanglement has some interesting properties and consequences. We won't get into them in this module, but more information can be found in module "Entanglement and EPR".
In order to have a quantum computer, we need gates that act not only on one qubit, but gates that work on multiple qubits. More specifically, we need gates that will "entangle" two qubits. The most common gate of this type is called the CNOT, or controlled-NOT gate. It does exactly as the name suggests: performs a NOT gate controlled by another qubit. The following is the circuit diagram for a CNOT gate:

The solid black dot on the top 'wire' indicates that this is the control qubit. The gate on the second qubit will be performed only if the control qubit is a 1. (This has interesting effects for superposition states, as we see in the clicker questions below!)
We can define how the CNOT gate acts on the four 2-qubit computational basis states:
$$ CNOT\ket{00} = \ket{00} \;\;\;\; CNOT\ket{01} = \ket{01}$$
$$ CNOT\ket{10} = \ket{11} \;\;\;\; CNOT\ket{11} = \ket{10}$$
We can use the CNOT to entangle two independent qubits as in the circuit in the clicker question example below.
Sample related online Tutorial:
An online introduction/tutorial on CNOT gates and entanglement is available on acephysics.net:
https://acephysics.net/tutorials/cnot-entanglement
An alternative set of basis states for 2-particle systems which is convenient when describing entangled systems is the "Bell basis", defined as
$\ket{\beta_{00}} \equiv \frac{1}{\sqrt{2}}(\ket{00} + \ket{11})$
$\ket{\beta_{01}} \equiv \frac{1}{\sqrt{2}}(\ket{01} + \ket{10})$
$\ket{\beta_{10}} \equiv \frac{1}{\sqrt{2}}(\ket{00} - \ket{11})$
$\ket{\beta_{11}} \equiv \frac{1}{\sqrt{2}}(\ket{01} - \ket{10})$
This basis is complete and orthonormal. The naming convention is not immediately obvious but can be understood when considering a simple conventional "entangling circuit" (the example from the clicker question in the "CNOT" section above).
Note: For spin-1/2 systems, the last state, $\ket{\beta_{11}}$ is a total spin-0 singlet, with interesting properties for e.g. Bell tests. More discussion of the Bell basis states happens in the "Entanglement and EPR" module.
$\ket{\beta_{10}} \doteq \frac{1}{\sqrt{2}}\begin{pmatrix} 1\\ 0\\ 0\\ -1 \end{pmatrix}, \ \ \ket{\beta_{11}} \doteq \frac{1}{\sqrt{2}}\begin{pmatrix} 0\\ 1\\ -1\\ 0 \end{pmatrix}$
More discussion of this type is in the "Entanglement and EPR" module.
An important part of quantum theory is the fact that you cannot copy an arbitrary quantum state. The proof (by contradiction) is relatively straightforward:
Assume you have a 'cloning machine'. Such a machine would take an unknown state $\ket{\psi}$ and a blank state (let's call it $\ket{b}$) and turn it into two copies of $\ket{\psi}$. Mathematically, we write it as: $U_{clone} (\ket{\psi} \otimes \ket{b}) = \ket{\psi} \otimes \ket{\psi} $

Since we want to be able to clone an arbitrary state, the cloning machine should also work if we input the state $\ket{\phi}$: $U_{clone} (\ket{\phi} \otimes \ket{b}) = \ket{\phi} \otimes \ket{\phi} $
We want to take the inner product of the two equations:
$$ [(\bra{\phi} \otimes \bra{b}) U_{clone}^\dagger ] [U_{clone} (\ket{\psi} \otimes \ket{b})] = [\bra{\phi} \otimes \bra{\phi} ] [ \ket{\psi} \otimes \ket{\psi}] \label{cloneeqn}$$
- $U_{clone}^\dagger U_{clone} = 1$ since $U$ is unitary
- Make sure to take the inner product of qubit 1 (from eqn 1) with qubit 1 (from eqn 2) and then for qubit 2 (from eqn 1) with qubit 2 (from eqn 2)
Then we have that:
$ \ip{\phi}{\psi} \ip{b}{b} = \ip{\phi}{\psi} \ip{\phi}{\psi} $
$ \ip{\phi}{\psi} = \ip{\phi}{\psi}^2$
This is only true if $\ip{\phi}{\psi}$ is equal to 1 or 0. Meaning the cloning machine will only work for states that are identical or orthogonal. In other words, you can build a cloning machine, but it will only clone a set of basis states, not an arbitrary superposition of those basis states.
Quantum teleportation is an example of using entanglement as a resource. The idea is to take a qubit at one location, and transport all information of that state to a second location (without physically moving the initial particle through the intermediate space.)
Some notes about teleportation:
- We are not making a clone. The initial state is destroyed in the process.
- The person "sending" the qubit does not gain any information about the state they are teleporting.
- The two parties require a shared entangled system before teleportation can happen.
- During teleportation, two classical bits (00, 01, 10, or 11) are transported. This means that no information can be sent faster than classical information can be transmitted (thus limited by the speed of light).
A circuit diagram representation of the process is shown below. 
Alice posses a "secret" qubit she wishes to teleport to Bob. This could be for communication, encryption, or e.g. as a means to transport qubits long distances in the context of a quantum computer. Alice need not know what the "secret" state is.
Preparation: Alice and Bob need to share a two-qubit entangled state $\beta_{00}$, such that Alice has the first qubit and Bob has the second. Alice thus possesses two qubits (the secret qubit and her half of the original entangled state), and Bob has the second qubit of the original entangled state.
Algorithm: The circuit above shows the algorithm, which involves the following steps.
- Alice runs her 2 qubits through the circuit shown above, effectively entangling her two bits. Note that this type of circuit was discussed in the preceding sections on "Entangling gates" and "Bell States".
- She follows this by a measurement of the two output bits, which results in one of 4 possibilities: 00, 01, 10, or 11.
- She transmits this information through a classical channel to Bob (thus, limiting the process to speed-of-light communication).
- Bob uses the information to run his single qubit through one of four gate choices (X, Y, Z, or 1) depending on which classical information he received (Details in our downloadable lecture notes).
- The output from this final gate is now the original secret qubit state.
The probabilities of the 4 measurement outcomes that Alice can get are all 25%, so she has gained no information. Bob has not yet made a measurement; he possesses a qubit in the same state as the original secret one, which can now be used for further purposes. An interesting side note: if the original secret bit was entangled with yet other qubits, the outcome of the process results in Bob's output bit entangled in the same way with those other qubits.
 Material Downloads
Material Downloads
We have a set of clicker questions and homework questions that can be adapted for use in your classroom, including transitioning some questions to group whiteboard activities or group exams.
Our classroom implementations of these materials, with our lecture notes and the set of clicker questions, homework, and exam questions we used are found in the "DOWNLOAD ALL" zip file below.
 Clicker Questions for Qubits, Quantum Gates, and Teleportation
Clicker Questions for Qubits, Quantum Gates, and Teleportation 
 Homework for Qubits, Quantum Gates, and Teleportation
Homework for Qubits, Quantum Gates, and Teleportation 
 Exam questions for Qubits, Quantum Gates, and Teleportation
Exam questions for Qubits, Quantum Gates, and Teleportation 
 Notes for Faculty
Notes for Faculty 
 DOWNLOAD ALL (including our implementation)
DOWNLOAD ALL (including our implementation) 
(For more information on how we implement these types of materials in our upper-division classes, see our related AJP paper.)
 Online Resources
Online Resources
We have developed a series of online tutorials that students can complete in class (alone or in groups) or at home. These materials are hosted on our homegrown website AcePhysics.net/QIS.
Links for specific tutorials include:
- Introduction to Quantum Gates - a first step in learning about quantum computing
- Quantum Circuit Diagrams - practice with single-qubit gates represented as circuit diagrams
- Tensor Products - helping students describe systems with multiple qubits
- CNOT and Entanglement - an introduction to the Controlled NOT (CNOT) gate and the related concept of entanglement.
If you are assigning this activity in your course, email us at hello[at]acephysics[dot]net to get a course page where you can access student completion information.
For more information on how we implement these types of materials in our upper-division classes, see our related AJP paper.
Explore other topics within QIS for QM
Introductory Quantum Information Science Materials
Who is this for? These materials are for anyone teaching an introductory (first course in) quantum computing or quantum information science.
Why did we create these materials?
- To assist faculty aiming to incorporate more active learning elements into their classes.
- To support students from multiple different academic backgrounds (physics, computer science, engineering, math, chemistry,...)
Why these topics? We focus on just a few fundamental ideas in QIS. Some students may find these materials too easy, while others may find them too hard. That is exactly the reason for their existence! The goal is to provide students with deep conceptual practice, allowing all students to reach a level of understanding that will set the foundation for future QIS learning.
What will you find here?
- Links to free online tutorials (interactive worksheets that provide students with real-time feedback as they practice, suitable for homework or in-class group work.
- Paper versions of those same tutorials, for use in class
- Clicker questions (conceptual questions that can be used to make your lectures more interactive)
 Introduction to Quantum Gates
Introduction to Quantum Gates
Content: Superposition states, single-qubit gates (X, Z, H, and I), Dirac and matrix notation, measurement probabilities, and single-qubit X, Z, H, and I gates.
Prerequisite knowledge: None. However, previous classroom introduction to basic ideas and notation of quantum states (including Dirac and matrix notation) is useful.
Faculty notes: See the first 4 entries in "Notes for Faculty" in our QIS for QM tab labeled "Qubits, Quantum Gates, ...": (1. Motivation, 2. Qubits, 3. Parts of a Computer, and 4. Quantum Gates)
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/introduction-to-quantum-gates - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
- "Clicker questions:" Editable in-class conceptual questions with instructor notes in PowerPoint format. (Download below)
 1. Screenshot of online activity
1. Screenshot of online activity 2a. Introduction to Quantum Gates (paper version)
2a. Introduction to Quantum Gates (paper version) 
 2b. Instructor's Guide to paper version
2b. Instructor's Guide to paper version 
 3. Clicker questions - Intro to Quantum Gates
3. Clicker questions - Intro to Quantum Gates 
 Quantum Circuit Diagrams
Quantum Circuit Diagrams
Content: Practice with single-qubit gates represented as circuit diagrams
Prerequisite knowledge: Basic gates and quantum states. (This can all be found in the previous tutorial, "Introduction to Quantum Gates.")
Faculty notes: See the fifth entry under "Notes for Faculty" in our QIS for QM tab labeled "Qubits, Quantum Gates, ...": (5. Circuit Diagrams)
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/quantum-circuit-diagrams - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
- "Clicker questions:" Editable in-class conceptual questions with instructor notes in PowerPoint format. (Download below.)
 1. Screenshot of online activity
1. Screenshot of online activity 2a - Paper Activity - Intro to Quantum Circuits
2a - Paper Activity - Intro to Quantum Circuits 
 2b. Instructor's Guide - Quantum Circuit Diagrams
2b. Instructor's Guide - Quantum Circuit Diagrams 
 Tensor Products
Tensor Products
Content: Helping students describe systems with multiple qubits
Prerequisite knowledge: Students should be familiar with quantum states, basic single-qubit gates and circuit diagram conventions. (i.e., The sections above, on this page.)
Faculty notes: See the sixth entry under "Notes for Faculty" in our QIS for QM tab labeled "Qubits, Quantum Gates, ..." : (6. Tensor products of states and operators)
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/tensor-products - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
 1. Screenshot of online activity
1. Screenshot of online activity 2a. Tensor Products Paper Activity
2a. Tensor Products Paper Activity 
 2b. Instructors guide - Tensor Products
2b. Instructors guide - Tensor Products 
 CNOT and entanglement
CNOT and entanglement
Content: An introduction to the controlled-NOT (CNOT) gate and the related concept of entanglement.
Prerequisite knowledge: Students should be familiar with quantum states, basic single-qubit gates and circuit diagram conventions, and the tensor product. (i.e., The previous sections on this page.)
Faculty notes: See entries 7-8 under "Notes for Faculty" in our QIS for QM tab labeled "Qubits, Quantum Gates, ...": (7. Definition of Entanglement and 8. Entangling gates/CNOT)
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/cnot-entanglement - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
 1. Screenshot of online activity
1. Screenshot of online activity 2a. Paper worksheet - CNOT and Entanglement
2a. Paper worksheet - CNOT and Entanglement 
 2b. Instructor's Guide - CNOT and Entanglement
2b. Instructor's Guide - CNOT and Entanglement 
 Quantum Cryptography (BB84)
Quantum Cryptography (BB84)
Content: This activity takes students through the BB84 quantum key distribution protocol. It uses quantum circuit notation and includes the effect of an eavesdropper.
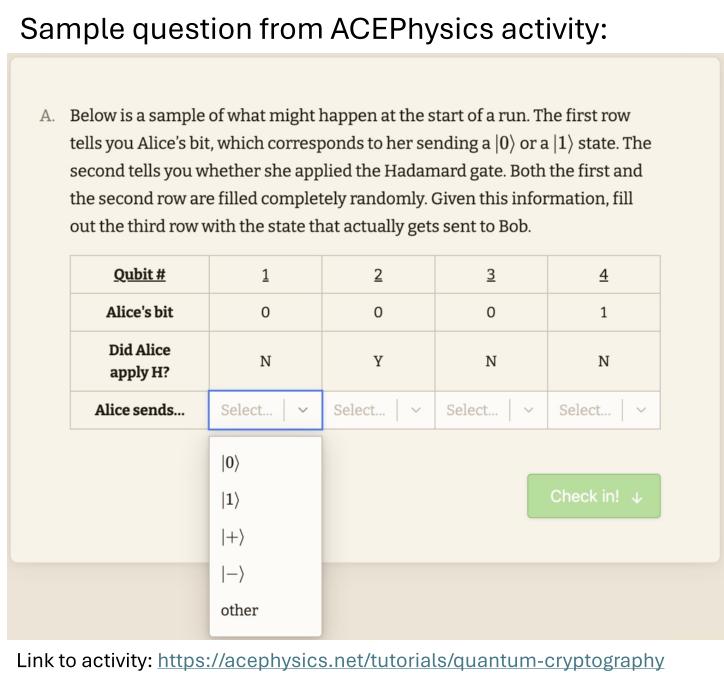
Prerequisite knowledge: Basic single qubit gates (in particular, the Hadamard, H gate). Students should know how to predict probabilistic outcomes of measurements in the computational (Z) basis on superpositions of $|0\rangle, |1\rangle, |+\rangle, |-\rangle$ states.
Faculty notes: See the "Notes for Faculty" in our QIS for QM tab: Quantum Cryptography
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/quantum-cryptography - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
 1. Screenshot of online activity
1. Screenshot of online activity 2a. Paper activity - Quantum Cryptography
2a. Paper activity - Quantum Cryptography 
 2b. Instructor's Guide - Quantum Cryptography
2b. Instructor's Guide - Quantum Cryptography 
What if I need help implementing active learning in my class?
Physport.org has some short guides to help you facilitate in-class tutorials, as well as to help you implement clicker questions in lectures effectively.)
Conceptual Assessment for Quantum Computing (QCCS)
|
We have developed a 20-question conceptual assessment that targets the introductory content in a quantum computing course (known as the QCCS). The survey is not designed to assess individual students but rather the course as a whole. The general content covered in the assessment includes mathematical foundations, superposition and measurement, quantum gates and circuit diagrams, and entanglement. The questions are conceptual in nature (not computational). Want to give the assessment to your students? |
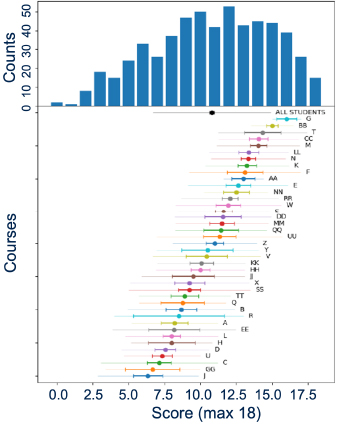 |
| Figure: Aggregated results for 568 students in a beta test of the QCCS across 40 different courses. Averages for each course is shown below the histogram, we see wide variation across classes, populations and pedagogical approaches. |
Who we are
We are PER research faculty teaching at very different institutions - different in class sizes and setups, student demographics, institutional research-focus - but all interested in helping introduce undergraduates to basic elements of Quantum Information Science. We have all taught a variety of quantum courses for many years.
The materials you will find here are not meant to be taken as givens, this is not a "fixed curriculum" that you are supposed to fully adopt (or reject). We hope that you will be inspired by some of the activities, notes, concept-tests, homeworks and more, and will borrow and adapt them for your own situation and students. We do not all use exactly the same materials ourselves.
We have borrowed where we can from PER literature on Quantum Mechanics (and tried - but apologize up front where we occasionally have failed - to appropriately credit the the hard development work of others!) We do not claim that these materials are "Research-validated" (they are still under development), but cheerfully present sometimes half-baked or partially-tested materials that we might argue are "research-based", a vaguer but perhaps more realistic description.
We welcome feedback and suggestions. If you make significant changes or additions, and particularly if you have classroom evidence that suggests it works well - let us know. We hope someday this site will be flexible enough to allow for community-sharing of new resources, and will work towards making that happen. (See contact information below.)
 |
Gina Passante is Associate Professor of Physics and Director of the Catalyst Center for the Advancement of Research in Teaching and Learning Math and Science at Cal State University Fullerton. She received her Ph.D. in quantum computing at U. Waterloo before transitioning to PER. |
 |
Steve Pollock is a Physics professor at CU Boulder who has engaged in PER for 20+ years. He has a background in theoretical nuclear physics. He is an APS Fellow, and was named US Professor of the Year in 2013. His PER work is focused on assessment and curricular materials development in upper-division physics courses. Please email if you are interested in teaching materials for other courses (including middle division Classical Mechanics, E&M, and others). He can be reached at Steven.Pollock (at) Colorado.edu |
 |
Bethany Wilcox is a Physics professor at CU Boulder. Her PER work focuses on the development of research-based and validated assessments of student learning that can be used to measure the impact of curricular changes or compare student learning across courses and institutions. In particular, she is utilizing advanced testing theories to explore viable options for creating modular assessments that can address variations in content coverage in across courses. |
We acknowledge the hard work of our students, including Josephine Meyer (University of Colorado Boulder), Jonan-Rohi Plueger (University of Colorado Boulder), and Bianca Cervantes (former California State University, Fullerton).
We are funded in part by NSF DUE- 2012147 and 2011958: Collaborative Research: Connecting Spins-First Quantum Mechanics Instruction to Quantum Information Science
PLEASE USE AND ADAPT whatever is helpful to you, however it will most benefit your students. Please credit our work if you share your materials beyond your own classes. Please make an effort to keep assessment materials off the open web - alter questions for your students.

 Entanglement and EPR
Entanglement and EPR Quantum Cryptography
Quantum Cryptography