Adaptable Curricular Exercises (ACE) for Quantum Information Science (QIS)
Our goals for this site are to provide adaptable resources to support faculty, including those very new to these topics, who wish to add some student-centered, research-based QIS instruction to your classes.
We have materials for two different audiences, depending on the type of course you teach.
QM Course: Are you teaching quantum mechanics in a physics department to (mostly) majors, and want to add a short unit on quantum information (e.g. quantum computing or cryptography) within your course?

QIS Course: Are you teaching a quantum computing/QIS course to a diverse population of students (e.g. computer science, physics, engineering, math...), and want to support students in the basic quantum mechanics needed?
(These materials are under development)
And: if you teach undergraduate quantum mechanics to physics students and are looking for a suite of student-centered materials to help you with the entire QM course, please visit our Adaptable curricular materials for Quantum Mechanics site.
Tools for introducing QIS in a QM course
Who is this for? An instructor teaching Quantum Mechanics who would like to add some quantum information science topics to their physics course.
(Materials are suitable for faculty new to these topics.)
Topics: We have divided our materials into three main topical areas.
Each is standalone - materials can be taught without any prerequisite material from the other groups.
(Because of this, there are some duplicate materials across the groups.)
We do not intend for the materials to be used wholly as written. Rather, they form a complete set that a faculty member can pick and choose from as it fits their schedule, the material already taught, and the interests of both the faculty member and student.
Types of instructional materials
The “instructional materials” found on this site include: lecture notes for faculty, concept tests, homework questions, online tutorials, and assessments.
Please use and adapt whatever is helpful to you, however it will most benefit your students. Please credit our work if you share your materials beyond your own classes. Please make an effort to keep assessment materials off the open web - alter questions for your students.
 Example Classroom Implementations
Example Classroom Implementations
Curriculum designers Dr. Steven Pollock and Dr. Gina Passante have each taught this material in their classes. Feel free to download our lecture notes - we are happy for you to use whatever material works for your class.
Please email if you try our materials and have any feedback:
steven.pollock (at) colorado.edu or gpassante (at) fullerton.edu
Steven Pollock's CU Boulder Implementation
CUB is a research-intensive public institution. I teach these materials in junior or senior-level undergraduate quantum mechanics courses, which currently all follow a spins-first curriculum (using McIntyre's Quantum Mechanics textbook.)
Each sequence below takes me one week. These are all taught in "large lecture" (75+ student) settings with three 50-minute lectures/week.
- I teach entanglement and EPR midway through the first semester (this is largely following McIntyre's Chapter 4 treatment)
- I teach qubits and teleportation late in the second semester (senior-level) quantum course, as a basic introduction to quantum information science. (This is largely following McIntyre's Chapter 16 treatment)
Please reach out if you have questions or feedback: steven.pollock (at) colorado.edu
Gina Passante's CSUF Implementation
CSUF is a primarily undergraduate, large, Hispanic-serving institution. I teach these materials in several of my quantum mechanics courses at the undergraduate and master's levels.
- Qubits, Quantum Gates, and Teleportation: I choose to teach this in the middle of a first semester of undergraduate QM. My course is spins-first and I do a "quantum computing" week to apply what they have learned before moving to position wave functions.
- Entanglement and EPR: I teach an introduction to entanglement and a conversation of "spooky action at a distance" when I teach the "qubits, quantum gates, and teleportation" material. But the discussion about the EPR paradox and the Bell inequalities is taught at the master's level.
- Quantum Cryptography: This is a one-class supplement that can be taught at any level. The only prerequisite knowledge is superposition states, measurement, and bra-ket notation. The example here was done in my first-semester, junior-level quantum mechanics course.
Feel free to reach out if you have questions (gpassante at fullerton dot edu).
 Quantum Cryptography
Quantum Cryptography
What is colloquially called "quantum cryptography" is more accurately described as "quantum key distribution" (QKD), where a secret key is distributed to two parties in a way that guarantees security. That key can then be used in one-time pad encryption.
These materials are intended for a faculty member to select and adapt relevant pieces to use in their classroom.
In our courses, this module takes one lecture to cover.
 Notes for Faculty - Quantum Cryptography
Notes for Faculty - Quantum Cryptography
We have written brief notes on the topics in this module that are intended for faculty adopters.
Browse below, or download all as a single pdf file (see Materials Download section below)
Topics include:
The one-time pad is a perfectly secure way to encrypt information. In this protocol, both parties must share a secret key. The one-time pad security relies on the fact that this key is truly secret (no one else has access to it) and that it is only used a single time (hence the name ``one-time''). The secret key must be at least as long as the message (no portion of the key should be repeated).
If Alice wishes to send a message to Bob, Alice will take the message and add the secret key to obtain the cyphertext (the encoded message). In the case of a binary message and a binary key, this would be addition mod 2.
$ \text{message} \oplus \text{key} = \text{cyphertext} $
In mod 2, Bob will just need to do $\text{cyphertext} \oplus \text{ key} = \text{message}$ to decode the cyphertext.
We will often do examples using the english alphabet, in which the addition will be modulo 26. In this case, to decode the cyphertext you will need to ${\it subtract}$ the key (mod 26) to obtain the message.
In all QKD protocols, it is an important assumption that an eavesdropper cannot copy (or clone) an unknown quantum state. The proof (by contradiction) is relatively straightforward:
Assume you have a 'cloning machine'. Such a machine would take an unknown state $\ket{\psi}$ and a blank state (let's call it $\ket{b}$) and turn it into two copies of $\ket{\psi}$. Mathematically, we write it as: $U_{clone} (\ket{\psi} \otimes \ket{b}) = \ket{\psi} \otimes \ket{\psi} $

Since we want to be able to clone an arbitrary state, the cloning machine should also work if we input the state $\ket{\phi}$: $U_{clone} (\ket{\phi} \otimes \ket{b}) = \ket{\phi} \otimes \ket{\phi} $
We want to take the inner product of the two equations:
$$ [ ( \bra{\psi} \otimes \ket{b} ) U_{clone}^\dagger ] [U_{clone} ( \ket{\psi} \otimes \ket{b} ) ] = [ \bra{\phi} \otimes \bra{\phi} ] [ \ket{\psi} \otimes \ket{\psi} ] \label{cloneeqn}$$
- $U_{clone}^\dagger U_{clone} = 1$ since $U$ is unitary
- Make sure to take the inner product of qubit 1 (from eqn 1) with qubit 1 (from eqn 2) and then for qubit 2 (from eqn 1) with qubit 2 (from eqn 2)
Then we have that:
$ \ip{\phi}{\psi} \ip{b}{b} = \ip{\phi}{\psi} \ip{\phi}{\psi} $
$ \ip{\phi}{\psi} = \ip{\phi}{\psi}^2$
This is only true if $\ip{\phi}{\psi}$ is equal to 1 or 0. Meaning the cloning machine will only work for states that are identical or orthogonal. In other words, you can build a cloning machine, but it will only clone a set of basis states, not an arbitrary superposition of those basis states.
This is one of the more common QKD protocols and is perfect for use in intro quantum mechanics classes as it only requires knowledge of two-level superposition states and the results of measurements.
In our example, we will use spin-1/2 particles, and we will discuss measurements of spin in the $x$ and $z$ directions.
Players:
Alice - Wants to share a secret key with Bob. She sends qubits to Bob, randomizing what she ends.
Bob - Wants to share a secret key with Alice. Bob receives the qubits sent by Alice and will measure them in a randomly chosen basis.
Eve - An eavesdropper who wants to gain information about the secret key without being detected. She will intercept the qubits that Alice sends to Bob and make measurements before sending the qubit on to Bob.
The Protocol: The following steps can be recorded in the handout (available for download below).
- Alice sends qubits to Bob in either the X or the Z basis. She randomly sends one of
$ \ket{\psi_{0z}}=\ket{0} \;\;\quad \quad \ket{\psi_{0x}}= \ket{+} = \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) $
$ \ket{\psi_{1z}}=\ket{1} \;\;\quad \quad \ket{\psi_{1x}}= \ket{-} = \frac{1}{\sqrt{2}}(\ket{0} - \ket{1}) $
Alice records the basis she sent (X or Z) and whether she sent the (0 or 1) for each basis. The sequence of 0s and 1s will turn into the secret key. - Bob receives the qubits and makes a measurement. He randomly chooses to measure in either the Z or the X basis and records the results (0 or 1) and the basis he chose (X or Z).
- Alice and Bob reveal the basis they sent or measured. They do this publically. They will throw away all elements of their key (the 0s and 1s) where their basis choice did not match.
- Test for an eavesdropper: Once Alice and Bob have the remaining key, it should match perfectly. The only reason their keys might differ is if there was an eavesdropper messing things up or if there was some decoherence in their qubit channel. They select a portion of their key to compare publically (they will then need to throw away these elements of the key as they are no longer secret). If that portion of their keys is identical, they can feel confident that the rest of their key also matches. If their keys are not identical, they do not have confidence in the rest of their key and will abandon the protocol and start again.
In reality, anything can happen to the qubit as it travels from Alice to Bob. We are going to assume the worst: that a very powerful and quantum-savvy enemy has intercepted the qubit and knows enough of the protocol to make the best measurements they can before sending the qubit to Bob.
Here is the best that an eavesdropper can do:
- Measure the intercepted qubit in either the X or Z basis. Record everything.
- Send the resulting qubit to Bob.
You can follow along in the handout to see the repercussions of this interception. In short:
- Eve will randomly pick the "right" basis to measure in 50% of the time. When she does this, the state she sends to Bob will be unchanged from what Alice sent. In these instances, she is undetectable.
- The other 50% of the time, Eve will select the "wrong" basis (the basis that is opposite to what Alice sent). In these instances, by chance, Eve will get the same key value as Alice 50% of the time and get an opposing value 50% of the time.
- Altogether, Eve has a 25% chance of messing up each qubit that gets sent to Bob.
If Alice and Bob did not test for the presence of an eavesdropper, even with an error rate of 25%, Eve would certainly gain valuable information if Alice and Bob tried to use their "secret" key to encode a message.
 Material Downloads
Material Downloads
Note: sometimes we teach this material with lecture and handouts and other times we use a tutorial worksheet (both can be downloaded below). We have only one homework question for this content.
Our classroom implementations of these materials are found in the "DOWNLOAD ALL" zip file below.
 Handouts for Quantum Cryptography
Handouts for Quantum Cryptography 
 Homework for Quantum Cryptography
Homework for Quantum Cryptography 
 Tutorial for Quantum Cryptography
Tutorial for Quantum Cryptography 
 DOWNLOAD ALL (including our implementation)
DOWNLOAD ALL (including our implementation) 
 Online Resources
Online Resources
We have developed a series of online tutorials that students can complete in class (alone or in groups) or at home. These materials are hosted on our homegrown website AcePhysics.net/QIS.
- EPR and entangled states - this Tutorial is framed in a context of cryptography, following an E92 protocol, but in terms of content is much more targeted on Bell states, entanglement, and measurement. ( It would not be suitable to assign without some previous background lecturing on entanglement and Bell states involving spin-1/2 states )
- Quantum Cryptography: This activity takes students through the BB84 quantum key distribution protocol. It uses quantum circuit notation and includes the effect of an eavesdropper. It is framed in the language of quantum computing and gates, rather than generic spin 1/2 states, and would be suitable for an audience that has little background in quantum mechanics (e.g. computer science students)
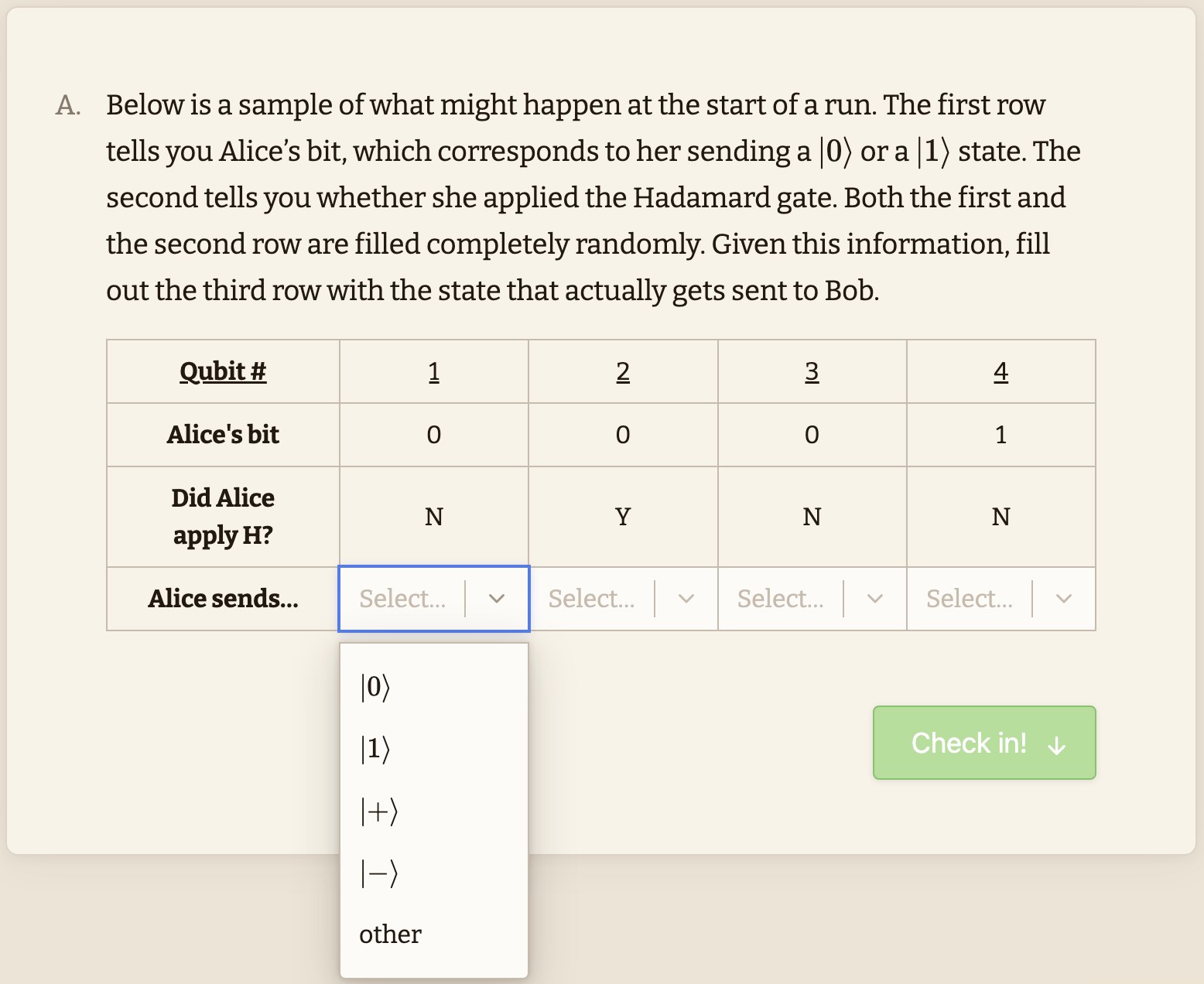
Prerequisite knowledge: Basic gates (H), measurements in the computational (Z) basis on the $|0\rangle, |1\rangle, |+\rangle, |-\rangle$ states.
If you are assigning this activity in your course, email us at hello[at]acephysics[dot]net to get a course page where you can access student completion information.
For more information on how we implement these types of materials in our upper-division classes, see our related AJP paper.
Explore other topics within QIS for QM
Introductory Quantum Information Science Materials
Who is this for? These materials are for anyone teaching an introductory (first course in) quantum computing or quantum information science.
Why did we create these materials?
- To assist faculty aiming to incorporate more active learning elements into their classes.
- To support students from multiple different academic backgrounds (physics, computer science, engineering, math, chemistry,...)
Why these topics? We focus on just a few fundamental ideas in QIS. Some students may find these materials too easy, while others may find them too hard. That is exactly the reason for their existence! The goal is to provide students with deep conceptual practice, allowing all students to reach a level of understanding that will set the foundation for future QIS learning.
What will you find here?
- Links to free online tutorials (interactive worksheets that provide students with real-time feedback as they practice, suitable for homework or in-class group work.
- Paper versions of those same tutorials, for use in class
- Clicker questions (conceptual questions that can be used to make your lectures more interactive)
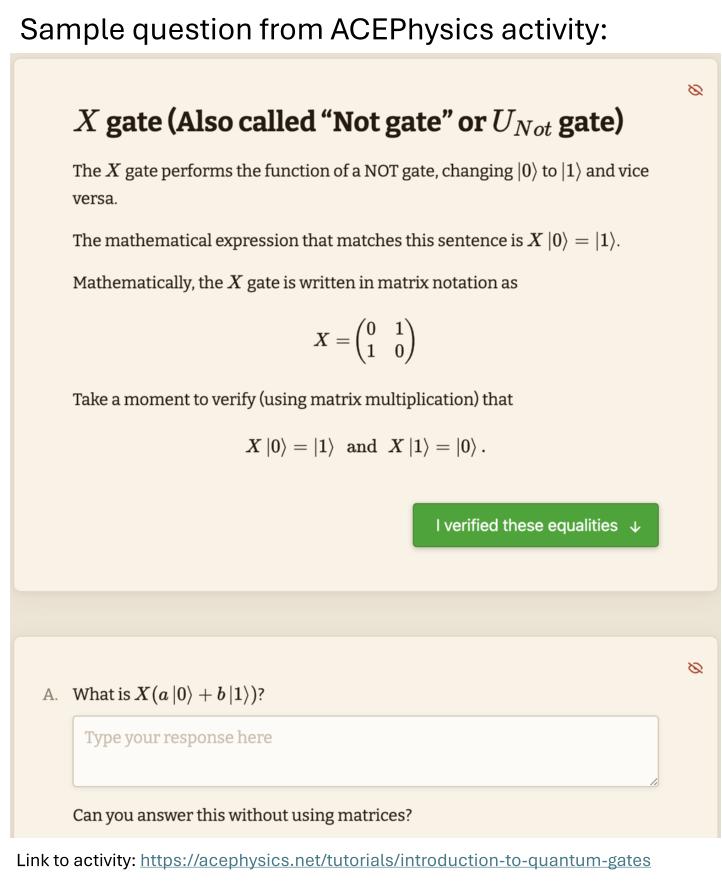
 Introduction to Quantum Gates
Introduction to Quantum Gates
Content: Superposition states, single-qubit gates (X, Z, H, and I), Dirac and matrix notation, measurement probabilities, and single-qubit X, Z, H, and I gates.
Prerequisite knowledge: None. However, previous classroom introduction to basic ideas and notation of quantum states (including Dirac and matrix notation) is useful.
Faculty notes: See the first 4 entries in "Notes for Faculty" in our QIS for QM tab labeled "Qubits, Quantum Gates, ...": (1. Motivation, 2. Qubits, 3. Parts of a Computer, and 4. Quantum Gates)
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/introduction-to-quantum-gates - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
- "Clicker questions:" Editable in-class conceptual questions with instructor notes in PowerPoint format. (Download below)
 1. Screenshot of online activity
1. Screenshot of online activity 2a. Introduction to Quantum Gates (paper version)
2a. Introduction to Quantum Gates (paper version) 
 2b. Instructor's Guide to paper version
2b. Instructor's Guide to paper version 
 3. Clicker questions - Intro to Quantum Gates
3. Clicker questions - Intro to Quantum Gates 
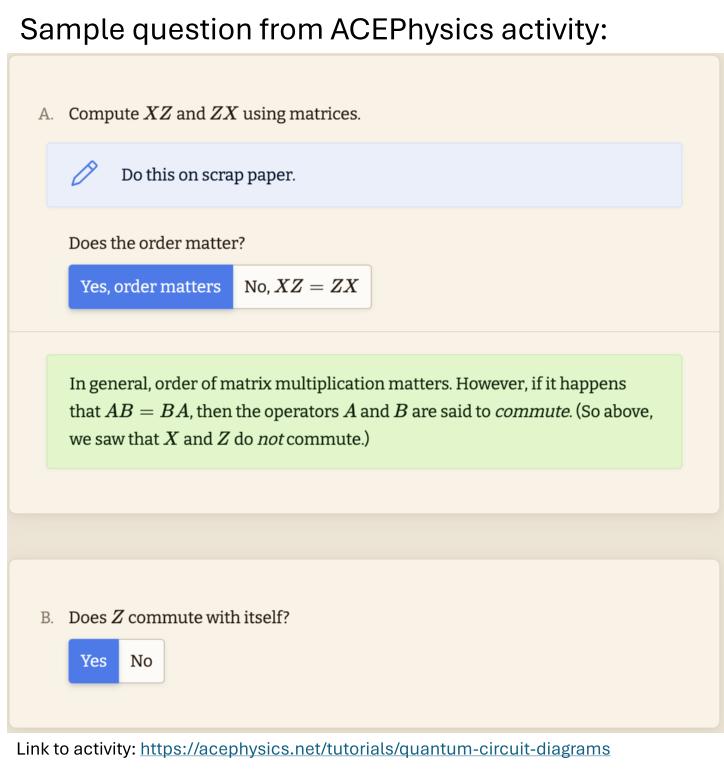
 Quantum Circuit Diagrams
Quantum Circuit Diagrams
Content: Practice with single-qubit gates represented as circuit diagrams
Prerequisite knowledge: Basic gates and quantum states. (This can all be found in the previous tutorial, "Introduction to Quantum Gates.")
Faculty notes: See the fifth entry under "Notes for Faculty" in our QIS for QM tab labeled "Qubits, Quantum Gates, ...": (5. Circuit Diagrams)
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/quantum-circuit-diagrams - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
- "Clicker questions:" Editable in-class conceptual questions with instructor notes in PowerPoint format. (Download below.)
 1. Screenshot of online activity
1. Screenshot of online activity 2a - Paper Activity - Intro to Quantum Circuits
2a - Paper Activity - Intro to Quantum Circuits 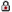
 2b. Instructor's Guide - Quantum Circuit Diagrams
2b. Instructor's Guide - Quantum Circuit Diagrams 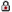
 Tensor Products
Tensor Products
Content: Helping students describe systems with multiple qubits
Prerequisite knowledge: Students should be familiar with quantum states, basic single-qubit gates and circuit diagram conventions. (i.e., The sections above, on this page.)
Faculty notes: See the sixth entry under "Notes for Faculty" in our QIS for QM tab labeled "Qubits, Quantum Gates, ..." : (6. Tensor products of states and operators)
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/tensor-products - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
 1. Screenshot of online activity
1. Screenshot of online activity 2a. Tensor Products Paper Activity
2a. Tensor Products Paper Activity 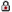
 2b. Instructors guide - Tensor Products
2b. Instructors guide - Tensor Products 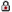
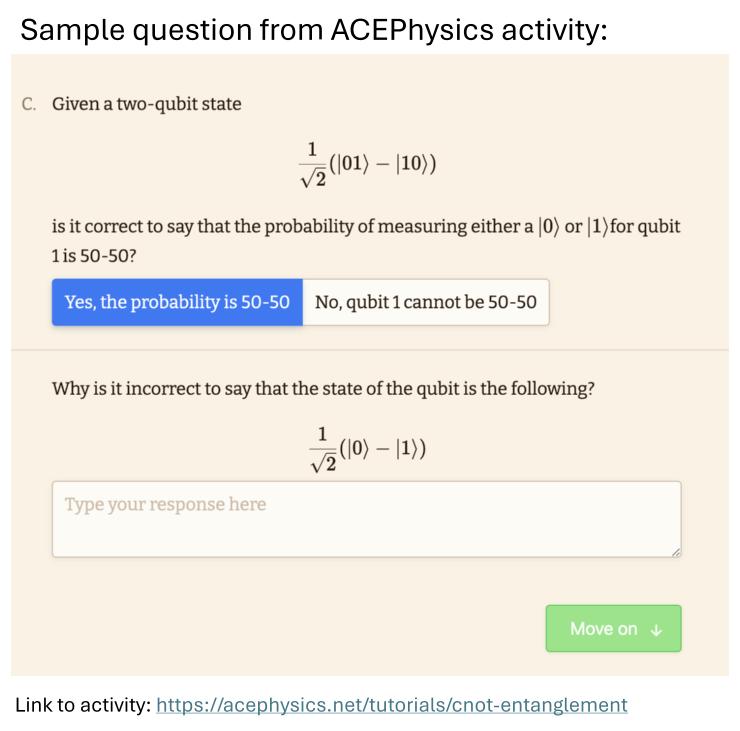
 CNOT and entanglement
CNOT and entanglement
Content: An introduction to the controlled-NOT (CNOT) gate and the related concept of entanglement.
Prerequisite knowledge: Students should be familiar with quantum states, basic single-qubit gates and circuit diagram conventions, and the tensor product. (i.e., The previous sections on this page.)
Faculty notes: See entries 7-8 under "Notes for Faculty" in our QIS for QM tab labeled "Qubits, Quantum Gates, ...": (7. Definition of Entanglement and 8. Entangling gates/CNOT)
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/cnot-entanglement - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
 1. Screenshot of online activity
1. Screenshot of online activity 2a. Paper worksheet - CNOT and Entanglement
2a. Paper worksheet - CNOT and Entanglement 
 2b. Instructor's Guide - CNOT and Entanglement
2b. Instructor's Guide - CNOT and Entanglement 
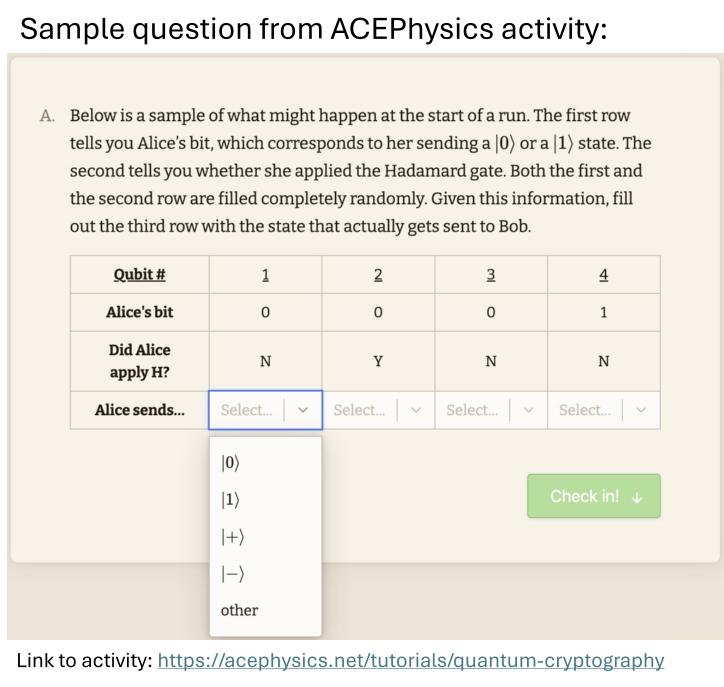
 Quantum Cryptography (BB84)
Quantum Cryptography (BB84)
Content: This activity takes students through the BB84 quantum key distribution protocol. It uses quantum circuit notation and includes the effect of an eavesdropper.
Prerequisite knowledge: Basic single qubit gates (in particular, the Hadamard, H gate). Students should know how to predict probabilistic outcomes of measurements in the computational (Z) basis on superpositions of $|0\rangle, |1\rangle, |+\rangle, |-\rangle$ states.
Faculty notes: See the "Notes for Faculty" in our QIS for QM tab: Quantum Cryptography
Materials available:
- AcePhysics online interactive tutorial - use this link:
acephysics.net/tutorials/quantum-cryptography - Paper worksheet: Paper version of the online tutorial for use in class with instructor supervision. (Download below, along with instructor notes for facilitation)
 1. Screenshot of online activity
1. Screenshot of online activity 2a. Paper activity - Quantum Cryptography
2a. Paper activity - Quantum Cryptography 
 2b. Instructor's Guide - Quantum Cryptography
2b. Instructor's Guide - Quantum Cryptography 
What if I need help implementing active learning in my class?
Physport.org has some short guides to help you facilitate in-class tutorials, as well as to help you implement clicker questions in lectures effectively.)
Conceptual Assessment for Quantum Computing (QCCS)
|
We have developed a 20-question conceptual assessment that targets the introductory content in a quantum computing course (known as the QCCS). The survey is not designed to assess individual students but rather the course as a whole. The general content covered in the assessment includes mathematical foundations, superposition and measurement, quantum gates and circuit diagrams, and entanglement. The questions are conceptual in nature (not computational). Want to give the assessment to your students? |
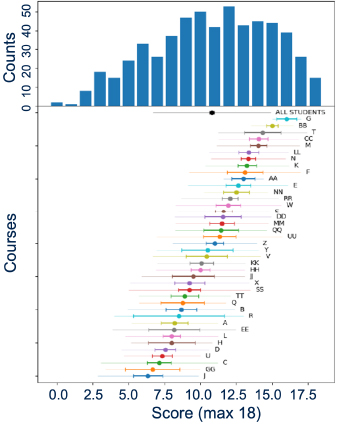 |
| Figure: Aggregated results for 568 students in a beta test of the QCCS across 40 different courses. Averages for each course is shown below the histogram, we see wide variation across classes, populations and pedagogical approaches. |
Who we are
We are PER research faculty teaching at very different institutions - different in class sizes and setups, student demographics, institutional research-focus - but all interested in helping introduce undergraduates to basic elements of Quantum Information Science. We have all taught a variety of quantum courses for many years.
The materials you will find here are not meant to be taken as givens, this is not a "fixed curriculum" that you are supposed to fully adopt (or reject). We hope that you will be inspired by some of the activities, notes, concept-tests, homeworks and more, and will borrow and adapt them for your own situation and students. We do not all use exactly the same materials ourselves.
We have borrowed where we can from PER literature on Quantum Mechanics (and tried - but apologize up front where we occasionally have failed - to appropriately credit the the hard development work of others!) We do not claim that these materials are "Research-validated" (they are still under development), but cheerfully present sometimes half-baked or partially-tested materials that we might argue are "research-based", a vaguer but perhaps more realistic description.
We welcome feedback and suggestions. If you make significant changes or additions, and particularly if you have classroom evidence that suggests it works well - let us know. We hope someday this site will be flexible enough to allow for community-sharing of new resources, and will work towards making that happen. (See contact information below.)
 |
Gina Passante is Associate Professor of Physics and Director of the Catalyst Center for the Advancement of Research in Teaching and Learning Math and Science at Cal State University Fullerton. She received her Ph.D. in quantum computing at U. Waterloo before transitioning to PER. |
 |
Steve Pollock is a Physics professor at CU Boulder who has engaged in PER for 20+ years. He has a background in theoretical nuclear physics. He is an APS Fellow, and was named US Professor of the Year in 2013. His PER work is focused on assessment and curricular materials development in upper-division physics courses. Please email if you are interested in teaching materials for other courses (including middle division Classical Mechanics, E&M, and others). He can be reached at Steven.Pollock (at) Colorado.edu |
 |
Bethany Wilcox is a Physics professor at CU Boulder. Her PER work focuses on the development of research-based and validated assessments of student learning that can be used to measure the impact of curricular changes or compare student learning across courses and institutions. In particular, she is utilizing advanced testing theories to explore viable options for creating modular assessments that can address variations in content coverage in across courses. |
We acknowledge the hard work of our students, including Josephine Meyer (University of Colorado Boulder), Jonan-Rohi Plueger (University of Colorado Boulder), and Bianca Cervantes (former California State University, Fullerton).
We are funded in part by NSF DUE- 2012147 and 2011958: Collaborative Research: Connecting Spins-First Quantum Mechanics Instruction to Quantum Information Science
PLEASE USE AND ADAPT whatever is helpful to you, however it will most benefit your students. Please credit our work if you share your materials beyond your own classes. Please make an effort to keep assessment materials off the open web - alter questions for your students.

 Qubits, Quantum Gates, and Teleportation
Qubits, Quantum Gates, and Teleportation Entanglement and EPR
Entanglement and EPR