The Physics Education Research group at the University of Colorado Boulder (PER@C) has developed and compiled resources for research-based instruction throughout the undergraduate curriculum. This includes materials developed as part of the CU Science Education Initiative and other research-based efforts, and materials developed later by other faculty at CU Boulder.
Requests when using and sharing:
On this site, you will find a number of materials we have borrowed or developed. Feel free to use what you like - we would like to share our materials, but also believe in giving credit to sources whenever possible (and ask that you do not use our materials for commercial purposes). We ask for your cooperation in not making any solutions you may create for the homework (and exam problems, clicker questions, etc…) available on the open web, out of respect for instructors and students at other institutions, and for maintaining the integrity of our research.
If you have questions, contributions, bug-catches, etc, please contact steven.pollock (at) colorado.edu Thanks!
Modern Physics is the third semester in our three-semester sequence of introductory physics courses.
- special relativity
- photoelectric effect
- spectra
- lasers
- Bohr and deBroglie models,
- Stern-Gerlach, entanglement and single-quanta experiments,
- matter waves and the Schrödinger equation,
- tunneling (α-decay, STM's),
- hydrogen atoms and molecular bonding,
- conductivity, semiconductors
- BECs.
Materials were originally developed for a course for engineering majors, with a focus on applications, in 2005 and 2006 by Wieman, Perkins, and McKagan (McKagan et al. 2007). They were later adapted for a course for physics majors to include special relativity by Finkelstein, Bohn, and later Rogers, Schibli, and Dessau. Finkelstein and Baily made further research-based adaptations to include content on quantum interpretation (Baily and Finkelstein 2010). Later updates by Finkelstein added a unit on diversity.
 Modern: MATERIALS DOWNLOAD
Modern: MATERIALS DOWNLOAD
The first set of materials is older, from the Science Education Initiative team (including C. Wieman, K. Perkins, S. McKagan, N. Finkelstein, and many others). It includes materials from multiple instutions dating back to 2009, and includes some homework and exam materials, lecture notes and slides, and more.
(We include this download for reference, but if you are looking for a more updated collection of materials to support your course, we recommend starting with the second set below.)
The second set of materials is from a more recent and updated implementation of the course at CU Boulder by Noah Finkelstein.
Requests when using and sharing:
On this site, you will find a number of materials we have borrowed or developed. Feel free to use what you like - we would like to share our materials, but also believe in giving credit to sources whenever possible (and ask that you do not use our materials for commercial purposes). We ask for your cooperation in not making any solutions you may create for the homework (and exam problems, clicker questions, etc…) available on the open web, out of respect for instructors and students at other institutions, and for maintaining the integrity of our research.
 Download_instructions_SEI_Modern
Download_instructions_SEI_Modern 
 Download_instructions_NF_materials
Download_instructions_NF_materials 
 Modern: Research-Based Assessment: QMCS
Modern: Research-Based Assessment: QMCS
Quantum Mechanics Conceptual Survey (QMCS) assesses conceptual material typically taught in modern physics. Topics include wave functions, probability, wave-particle duality, uncertainty principle, infinite square well, one-dimensional tunneling, energy levels. You can learn more and download the assessment from PhysPort using the link above.
 Modern: About the Course
Modern: About the Course
The archived modern physics materials are available together as a package in the Materials tab. The course calendar below (for SP11 - with SR) is the simplest way to browse the most current materials.
NOTE: the Materials download (above) contains the files.
- special relativity
- photoelectric effect
- spectra
- lasers
- Bohr and deBroglie models,
- Stern-Gerlach, entanglement and single-quanta experiments,
- matter waves and the Schrödinger equation,
- tunneling (α-decay, STM's),
- hydrogen atoms and molecular bonding,
- conductivity, semiconductors
- BECs.
Written homework was assigned on Tuesdays, and due at the beginning of class on the Thursday in the following week (i.e., 10 days later). Students were expected to complete the readings before the lecture.
| WEEK |
Tuesday Lecture | Thursday Lecture | Homework |
|
1 |
(No class) | 1. Introduction, math review |
HW 1 |
|
2 |
2. E&M review, waves & wave equations |
3. Interference, polarization, |
HW 2 |
|
3 |
4. Michelson-Morley experiment, SR postulates |
5. Time dilation, length contraction |
HW 3 |
|
4 |
6. Lorentz transformations, spacetime, addition of velocities |
7. Relativistic momentum, energy |
No HW |
|
5 |
8. Modeling in physics, intro to quantum |
Exam 1 |
HW 4 |
|
6 |
9. Photoelectric effect 1 |
10. Photoelectric effect 2, photons |
HW 5 |
|
7 |
11. Photons, atomic spectra |
12. Lasers |
HW 6 |
|
8 |
13. Bohr model, de Broglie waves |
14. Stern-Gerlach experiments |
HW 7 + |
|
9 |
15. Repeated spin measurements, probability |
16. Entanglement, EPR, quantum cryptography |
HW 8 + |
|
10 |
17. Single-photon experiments, complementarity |
18. Electron diffraction, matter waves, |
HW 9 + |
|
11 |
19. Matter waves, Review for Exam 2 |
Exam 2 |
No HW |
|
12 |
20. Wave equations, Schrodinger equation, |
21. Infinite/finite square well, tunneling |
HW 10 |
|
13 |
22. Tunneling, alpha-decay |
23. Radioactivity, STM's |
HW 11 |
|
14 |
24. Hydrogen atom 1 |
25. Hydrogen atom 2 |
HW 12 |
|
15 |
26. Multi-electron atoms, periodic table, |
Exam 3 |
No HW |
|
16 |
27. Molecular bonding, Bose-Einstein Condensates |
Review |
(Final Exam) |
The online simulations listed below were used in both lectures and homeworks for the Spring 2011 modern physics course at CSM. Most of these links lead directly to the PhET Interactive Simulations project, online simulations developed at the University of Colorado, many of them specifically for this course. There are a number of sims for all kinds of quantum phenomena that we didn't use, as well as general physics content. We would also recommend the simulations from the The Quantum Mechanics Visualisation Project at the University of St Andrews.
Note that some older sims are java or flash. (Your mileage may vary running those on modern browsers - if you want to use these in classes be aware that e.g. some will not work on phones or pads)
Weeks 1-2: (Pre-Quantum)
- Standing Waves is a versatile wave sim. We used to recommend Walter Fendt's Standing Waves but it can be tricky to run on modern computers
- RadioWave Sim (E/M waves)
- Waves Sim (Water, Sound, E/M waves)
Special Relativity:
We're aware of only a few simulations for topics from special relativity [please let us know about ones you think are good]. The special relativity lecture slides (CSM SP11) are nicely animated, but not particularly interactive. We have not tested them with students, but there are some interesting visualizations at:
- A Slower Speed of Light - Developed by Gerd Kortemeyer (MSU) while on sabbatical at the MIT Game Lab
- Space Time Travel - Visualization of the theory of relativity - Universität Hildesheim (Germany)
- Real Time Relativity - Australian National University. Supporting AJP article here
Week 6:
Week 7:
- Lasers [the best of the bunch!!]
- Neon Lights & Other Discharge Lamps
- Quantum Wave Interference
Week 8:
Week 10:
Week 13:
Week 14:
 Modern: Learning Goals
Modern: Learning Goals
(This is an early draft from 2006)
Selected topical learning goals for Phys 2130
1. Wave function and probability
- Explain how the wave function description of matter replaces the particle description of matter.
- Determine a potential energy diagram from a physical situation and vice versa.
- Recognize that quantum mechanics describes the world using an energy picture rather than a force picture.
- Predict where a particle is most likely to be, given a wave function.
- Predict the energy that a particle is most likely to have, given a wave function.
- Apply the definitions of amplitude, wavelength, frequency for classical and quantum waves.
- Determine reflection and transmission coefficients for classical and quantum waves.
2. Wave-particle duality
- Recognize that matter is described by wave functions, not by particles moving along trajectories.
- Recognize that the wave function, via the Schrodinger Equation, describes the entire dynamics of matter, but cannot be measured.
- Recognize that light is described by electromagnetic waves.
- Compare and contrast the behavior of electromagnetic waves and matter waves.
- Recognize that light comes in discrete energy packets.
- Explain how the photoelectric effect experiment proves that light comes in discrete energy packets.
- Describe how energy quantization results from boundary conditions on wave functions or other kinds of waves.
- Determine when to use wave picture and when to use particle picture and recognize that it is not random.
- Describe how the wave picture of electrons leads to quantization of energy levels in atoms.
- Recognize that “Which slit did the particle go through?” in a double slit experiment is a trick question.
3. Schrodinger Equation
- Motivate the Schrodinger Equation from conservation of energy.
- Solve the Schrodinger Equation for simple potentials.
- Sketch solutions to the Schrodinger Equation for arbitrary potentials.
- Use the Schrodinger Equation to describe tunneling and radioactive decay.
- Calculate reflection and transmission coefficients, and determine how these change with width and height of barrier.
- Describe how the solutions to the Schrodinger equation explain the shape of orbitals of atoms.
- Describe how the solutions to Schrodinger explain the numbers of electrons in each shell of an atom.
4. Quantization of energy/quantum numbers/unique states
- Recognize that things can exist only in certain discrete states; not all values of energy, angular momentum, spin, etc. are possible.
- Describe how this quantization results from wave nature of matter.
- Recognize that when things exist in certain energy states, they take on certain probability distribution functions.
- Describe how quantization explains the structure of the periodic table.
- Predict occupancy of states based on the Pauli Exclusion Principle.
- Calculate the energies of photons emitted in transitions.
5.Uncertainty principle
- Recognize that a particle in an energy or momentum eigenstate is spread out in space.
- Recognize that a localized particle does not have a well-defined energy or momentum.
- Recognize that the uncertainty principle describes a fundamental indeterminacy, not just something that we don’t know.
- Describe how the uncertainty principle results from probabilistic interpretation of wave function.
6. Superposition
- Recognize that a system can be in superposition of eigenstates, and is not necessarily always in an eigenstate.
- Predict possible outcomes of a measurement of a superposition state.
7. Operators and observables
- Predict with what probability a certain value of an observable will be measured.
8. Measurement
- Determine how a quantum mechanical system changes upon measurement.
- Recognize that this behavior is NOT simply because a measurement “disturbs the system.”
- Recognize that “What was the energy before you measured it?” is a trick question.
- Recognize that a measurement is simply an interaction with something external to the system.
- Explain why and how measuring which slit the particles go through in a double slit experiment destroys the interference pattern.
- Recognize that an eigenstate is what you get when you make a measurement, not necessarily the state that things are always in.
 Modern: Student Challenges
Modern: Student Challenges
- Review of EM Waves (Sim: Radio Waves and Electromagnetic Fields)
- ~40% of class thinks charges moving at constant speed generate light (because charges in light bulb filament move at constant speed, because a spark is a charge moving at constant speed, because they don’t see why it wouldn’t).
- Many students think EM waves consist of something physically moving up and down in space, rather than fields increasing and decreasing in magnitude. We have clicker questions to address this. There is always some confusion over wording, but also real issues of students not understanding the physics.
- We review how classical EM wave energy independent of frequency because students don’t know classical model when we get to photoelectric effect.
- Photoelectric Effect (Sim: Photoelectric Effect)
This is a much harder topic for students than professors think. For details, see McKagan et al. 2009. Common student difficulties (many can be resolved with sim):- think voltage rather than light takes electrons off plate
- think current increases with speed of electrons
- can’t explain basic function of experiment
- can’t explain classical model of light
- can’t explain why PE experiment leads to photon model of light
- A general problem that first appears here is that some students have no ability to think hypothetically and can’t separate what was expected classically from what really happens.
- Probability and Randomness and Wave particle duality (Sim: Quantum Wave Interference)
- When we ask how students visualize light, ~40% have “Bohmian” view of particle traveling alongside EM wave.
- We use sim to demonstrate how the double slit experiment shows that light must be both a wave that goes through both slits and a particle that hits the screen at a single location. This lecture led to an unexpected onslaught of deep, fundamental questions that took up nearly an entire class period. Many students ask whether the particle is actually inside wave with a definition location that we just don’t know. Students get pretty frustrated with this class.
- Rutherford Scattering (Sim: Rutherford Scattering)
- In interviews we found that after instruction some students described the plum pudding model as cloud of negative charge filled with protons. They’re probably mixing it up with the Schrodinger model.
- In interviews we found that after instruction some students described the plum pudding model as cloud of negative charge filled with protons. They’re probably mixing it up with the Schrodinger model.
- Atomic Spectra and Discharge Lamps (Sim: Neon Lights & Other Discharge Lamps)
- We teach spectra before the Bohr model in order to emphasize how Bohr was able to explain the observed spectra with his model.
- Students often have trouble with the idea that the energy of light corresponds to the difference between the levels rather than the values of the levels. They need lots of explicit practice to get this distinction straightened out.
- We get lots of questions about how the electron chooses which level to jump down to, and how it decides when to jump down. These questions are useful later for emphasizing why the Schrodinger model of the atom is better than the Bohr model.
- The simulation and associated homework really help students build a clear model of how a discharge lamp work. The one place they had trouble was relating this model to what they see in a real discharge lamp, even though we did a demo with real discharge lamps and diffraction gratings. It’s important to be really explicit in this demo about how the physical lamps relate to the model in the sim.
- When reminding students of Coulomb potential energy, they remember the equation kq1q2/r, but often don’t realize that this is the same as –ke²/r.
- The idea of how fluorescent lights work is harder for students than you might think because they have trouble with the idea that red+blue+green light looks like white light to the eye. We get a lot of questions here about how the eye works.
- Lasers (Sim: Lasers)
- We originally covered Lasers towards the end of the course, but we realized that we didn’t actually use anything other than the basics of spectra in our treatment, and the engineers got grumpy if we spent too long on fundamentals without any applications, so we moved Lasers to so that there was more emphasis on applications early in the course. This worked much better.
- When we ask students why laser beams are so powerful, it’s split 50/50 between more power in the beam and more concentrated light.
- The homework on lasers starts with basic questions about absorption and spontaneous and stimulated emission, works through the steps of building a laser and troubleshooting a broken laser, and ends with essays on why a population inversion is necessary to build a laser and why this requires atoms with three energy levels instead of two. Most students are able to give coherent explanations in these essays. Students get less frustrated by the homework if it follows a lecture demo of the sim.
- Balmer Series
- We emphasize the point that Balmer came up with his formula by playing around with numbers and didn’t know what it meant. This is probably lost on students who think all of physics is like that.
- We emphasize the point that Balmer came up with his formula by playing around with numbers and didn’t know what it meant. This is probably lost on students who think all of physics is like that.
- Bohr and deBroglie Models of the atom (Sim: Models of The Hydrogen Atom)
- For details about why and how we teach this topic, see McKagan et al. 2008.
- This is really an opportunity to teach modeling and the significance of Bohr explaining where Balmer’s equation came from and deBroglie explaining why there are fixed energy levels. This is a really difficult section for students who have trouble thinking hypothetically.
- In the Bohr model, students often mix up total and potential energy, for example, thinking that -13.6eV is the potential energy. This confusion is confounded by the way the total energy lines are drawn on top of the potential energy curves.
- Double slit and Davisson Germer experiment (Sims: Quantum Wave Interference, Davisson Germer: Electron Diffraction)
- Students have a much harder time thinking of electrons as waves than photons, because electrons have mass.
- Students often think that the size of the wave packet, rather than the wavelength, should determine the spacing of the interference pattern.
- We have noticed that students often miss the point of the Davisson Germer experiment. They remember that electrons were only detected at certain angles, but cannot explain why. They view the electrons as particles that happen to bounce off at certain angles for some reason they can’t understand, rather than recognizing how the observations can be explained by the wave nature of electrons. We have found two things that really help to address this: (1) Start with a review of the double slit experiment, a context where students understand interference much better, talking about how you would like to do this to test deBroglie’s hypothesis, and then explain why this is really hard to do and then talk about how the Davisson Germer experiment is analogous. (2) Use the Davisson Germer sim to illustrate how wave interference leads to peaks in intensity at certain angles.
- Wave functions and probability
- When we first introduce wave functions with arbitrary functions, students often don’t recognize these as waves because they think “waves” are sine waves.
- “Wave number” is usually new and unfamiliar to students, and it’s worth spending 5 minutes to discuss why we define this quantity and how it relates to wavelength.
- Wave packets and uncertainty principle (Sims: Quantum Wave Interference, Quantum Tunneling and Wave Packets, Fourier: Making Waves)
- We introduce wave packets early because they are much more intuitive than plane waves and easier to relate to “particles.”
- We introduce wave packets early because they are much more intuitive than plane waves and easier to relate to “particles.”
- Wave equations and Differential equations
- It is worth emphasizing that the way we solve differential equations in physics, by just “guessing” the solution, is completely different from the way they have been taught to solve differential equations in math classes. Many students make this section way too hard by attempting to use complicated methods they have learned in math classes.
- It is worth emphasizing that the way we solve differential equations in physics, by just “guessing” the solution, is completely different from the way they have been taught to solve differential equations in math classes. Many students make this section way too hard by attempting to use complicated methods they have learned in math classes.
- Schrodinger equation for free particle (Sim: Quantum Tunneling and Wave Packets)
- You can use the Quantum Tunneling sim to demonstrate free particles by just setting the potential to “constant.”
- Students often have difficulty understanding the meaning of complex wave functions. This can perhaps best be illustrated by the observation that students frequently ask, “What is the physical meaning of the imaginary part of the wave function?” but never ask about the physical meaning of the real part, even though both have the same physical significance.
- Potential Energy
- We have found that without explicit instruction on how to relate potential energy diagrams to physical systems, most students don’t know what a potential energy diagram means or how it relates to anything real. When we do give explicit instruction on this, students start asking a lot of questions, and it becomes clear what a struggle it is for them to make sense of it.
- The fact that we often use the symbol V for potential energy and use the words “potential” and “potential energy” interchangeably leads to a lot of students thinking that V is actually the electric potential. It is worth emphasizing repeatedly that this is NOT what it means.
- Infinite and Finite Square Wells (Sim: Quantum Bound States)
- We illustrate a finite square well with the physical example of an electron in a short wire, and illustrate an infinite square well with the same system with a really big work function. We justify why this potential energy represents this system by building it up from a microscopic model of the atoms in the wire. Before we did this, we found that students often mixed up wells and barriers. Afterwards, this happened much less.
- The practice of drawing potential energy, total energy, and wave function on the same graph leads students to confuse these quantities. We have several clicker questions to elicit and address this confusion.
- Quantum Tunneling, Alpha decay and other applications of Tunneling (Sim: Quantum Tunneling and Wave Packets)
- Language such as “potential well,” “step,” and “barrier” often leads students to interpret potential energy diagrams as physical objects. It is worth pointing out that these words are only analogies, and using examples such as an electron tunneling through an air gap where there is clearly no physical barrier.
- There is a lot of research showing that students often believe that energy is lost in tunneling, and we have incorporated a tutorial and homework designed to address this belief. Two main reasons that students think this are that they mix up energy and wave function and interpret the exponential decay of the wave function as energy loss, or that they think of a classical object penetrating a physical barrier, in which case there is always dissipation. To address the first reason, we avoid drawing the wave function and the energy on the same graph, and ask several clicker questions designed to elicit and address this confusion. To address the second reason, we emphasize that there is no dissipation in the Schrodinger equation.
- While plane waves are mathematically simple, conceptually it is quite difficult to imagine a wave that extends forever in space and time, especially when it is tunneling. The language we use to describe tunneling is time-dependent. For example, we say that a particle approaches a barrier from the left, and then part of it is transmitted and part of it is reflected. This language is difficult to reconcile with a picture of a particle that simultaneously incident, transmitted, and reflected, for all time. We find that it works much better to start instruction with wave packets, using a qualitative description and the Quantum Tunneling sim, and then show how plane waves make the math easier.
- Determining the potential energy function for a physical example such as an STM or α decay actually requires understanding many steps and approximations, and is not trivial for students. If you simply present students with these potential energy functions, they usually don’t know how to relate them to the physical systems they are supposed to represent. We have many clicker questions designed to help students build a model for the potential energy functions for STMs and α decay.
- Reflection and Transmission (Sim: Quantum Tunneling and Wave Packets)
- There is a lot of math here and it’s very easy to get lost in the math and forget why you’re doing it. When asking students to work through it in homework, it’s very useful to ask them to stop after each step in the math and explain in words what they just did.
- There is a lot of math here and it’s very easy to get lost in the math and forget why you’re doing it. When asking students to work through it in homework, it’s very useful to ask them to stop after each step in the math and explain in words what they just did.
- Superposition, measurement, and expectation values (Sim: Quantum Bound States)
- Modern Physics textbooks typically do not cover superposition and measurement. We do, because it seems to us that if you don’t talk about measurement, you don’t know what you’re actually doing in QM or how it relates to the real world.
- We have chosen to cover expectation values in some semesters and not others. It helps to relate it to more familiar examples such as grade distributions and gambling.
- Hydrogen atom (Sims: Models of The Hydrogen Atom, Rutherford Scattering, Falstad quantum atom sim (not PhET))
- It is extremely important in this section to relate the Schrodinger model of the atom back to the discussion of models of the atom earlier in the course (section 8), and show how this is the next step in the progression of models. Otherwise, students are likely to view this section as just one more example of a solution of the Schrodinger equation and not realize that we are actually talking about another model of the atom.
- We have a homework in which we ask students to work through the simulations and explain the reasons for and limitations of each models. It’s amazing how difficult this is for students.
- Multielectron atoms
- We cover this topic very qualitatively, talking about how quantum mechanics explains the patterns in the periodic table, but not doing any calculations.
- We cover this topic very qualitatively, talking about how quantum mechanics explains the patterns in the periodic table, but not doing any calculations.
- Molecular bonding and solids (Sim: Quantum Bound States)
- Most engineers don’t seem very interested in learning the quantum mechanical basis of chemistry, and many complain that this is one of their less favorite topics.
- Most engineers don’t seem very interested in learning the quantum mechanical basis of chemistry, and many complain that this is one of their less favorite topics.
- Conductivity (Sim: Conductivity)
- This section is fairly straightforward and the engineers are usually familiar with band theory and interested in seeing how it relates to what they’ve learned in this class. However, they have often learned a very specific vocabulary for talking about bands, and get frustrated when our discussion is not consistent with this vocabulary.
- This section is fairly straightforward and the engineers are usually familiar with band theory and interested in seeing how it relates to what they’ve learned in this class. However, they have often learned a very specific vocabulary for talking about bands, and get frustrated when our discussion is not consistent with this vocabulary.
- Diodes and LEDs (Sim: Semiconductors)
- In the typical representation of diodes, excess filled energy levels above a gap are represented by –’s and empty energy levels below a gap are represented by +’s. This is extremely confusing and often leads students to believe that the –’s and +’s represent excess charges, which they do not. We have several clicker questions designed to help students see what’s going on here and correctly interpret this representation.
- In the typical representation of diodes, excess filled energy levels above a gap are represented by –’s and empty energy levels below a gap are represented by +’s. This is extremely confusing and often leads students to believe that the –’s and +’s represent excess charges, which they do not. We have several clicker questions designed to help students see what’s going on here and correctly interpret this representation.
- CCDs
- This topic was pretty complicated, and required a lot of steps to understand. The students complained that it was too hard. It probably would have been fine if we spent more time on it, but we had only one lecture and it was rushed.
- This topic was pretty complicated, and required a lot of steps to understand. The students complained that it was too hard. It probably would have been fine if we spent more time on it, but we had only one lecture and it was rushed.
- Spin and MRI (Sims: Stern Gerlach Experiment, Simplified MRI)
- We cover only enough details about spin to discuss MRI and EPR. All we really say is that it’s an additional quantum number than can be measured as up or down.
- Our treatment of MRI, and our simulation, closely follows the description given in Bloomfield’s textbook How Things Work.
- EPR paradox
- We have covered this topic in one day or two. One day is pretty rushed, but possible. Throughout the course, students have been asking whether the electron really goes through both slits or we just don’t know which it went through, whether it really has an undefined momentum when its position is known or we just don’t know what it’s position is, and other similar questions. In this lecture we finally answer those questions. Some students really love this lecture, and some find it confusing and don’t get it (there are a lot of steps of hypothetical reasoning in it). I don’t know what percentage of students falls into each category.
 Modern: Research Associated with the Course
Modern: Research Associated with the Course
The papers linked below explain much of the process and rationale behind the transformations. The first part (2006) reports on the state of affairs following the first year of the process, after the course had been taught twice (in the FA05 and SP06 semesters). The second part (2011) details additional changes that were made to the materials as part of Charles Baily's dissertation project on quantum perspectives.
- C. Baily, Perspectives in Quantum Physics: Epistemological, Ontological and Pedagogical, Ph.D., University of Colorado at Boulder, 2011.
- C. Baily and N. Finkelstein, Student Perspectives in Quantum Physics, presented at the Physics Education Research Conference 2008, Edmonton, Canada, 2008.
- C. Baily and N. Finkelstein, Development of quantum perspectives in modern physics, Phys. Rev. ST Phys. Educ. Res. 5 (1), 010106 (2009).
- C. Baily and N. Finkelstein, Quantum Interpretations in Modern Physics Instruction, presented at the Physics Education Research Conference 2009, Ann Arbor, Michigan, 2009.
- C. Baily and N. Finkelstein, Interpretation in Quantum Physics as Hidden Curriculum, presented at the Physics Education Research Conference 2010, Portland, Oregon, 2010.
- C. Baily and N. Finkelstein, Refined characterization of student perspectives on quantum physics, Phys. Rev. ST Phys. Educ. Res. 6 (2), 020113 (2010).
- C. Baily and N. Finkelstein, Teaching and understanding of quantum interpretations in modern physics courses, Phys. Rev. ST Phys. Educ. Res. 6 (1), 010101 (2010).
- C. Baily and N. Finkelstein, Interpretive Themes in Quantum Physics: Curriculum Development and Outcomes, presented at the Physics Education Research Conference 2011, Omaha, Nebraska, 2011.
- C. Baily and N. D. Finkelstein, Teaching quantum interpretations: Revisiting the goals and practices of introductory quantum physics courses, Phys. Rev. ST Phys. Educ. Res. 11 (2) 020124 (2015).
- L. Deslauriers and C. Wieman, Learning and retention of quantum concepts with different teaching methods, Phys. Rev. ST Phys. Educ. Res. 7 (1), 010101 (2011).
- S. McKagan, W. Handley, K. Perkins, and C. Wieman, A Research-based Curriculum for Teaching the Photoelectric Effect, Am. J. Phys. 77 (1), 87 (2009).
- S. McKagan, K. Perkins, M. Dubson, C. Malley, S. Reid, R. LeMaster, and C. Wieman, Developing and Researching PhET simulations for Teaching Quantum Mechanics, Am. J. Phys. 76 (4), 406 (2007).
- S. McKagan, K. Perkins, and C. Wieman, Reforming a large lecture modern physics course for engineering majors using a PER-based design, presented at the Physics Education Research Conference 2006, Syracuse, New York, 2006.
- S. McKagan, K. Perkins, and C. Wieman, Deeper look at student learning of quantum mechanics: The case of tunneling, Phys. Rev. ST Phys. Educ. Res. 4 (2), 020103 (2008).
- S. McKagan, K. Perkins, and C. Wieman, Why we should teach the Bohr model and how to teach it effectively, Phys. Rev. ST Phys. Educ. Res. 4 (1), 010103 (2008).
- S. McKagan, K. Perkins, and C. Wieman, Design and validation of the Quantum Mechanics Conceptual Survey, Phys. Rev. ST Phys. Educ. Res. 6 (2), 020121 (2010).
- S. McKagan and C. Wieman, Exploring Student Understanding of Energy through the Quantum Mechanics Conceptual Survey, presented at the Physics Education Research Conference 2005, Salt Lake City, Utah, 2005.
At CU Boulder, sophomore Classical Mechanics spans two semesters, explicitly adding coverage of a number of math tools that will be (re)encountered throughout the remainder of a typical physics major's career, introducing them in the context of Classical Mechanics.
Classical Mechanics/Math Methods 1 includes Newton's laws with velocity dependent forces, rockets, energy and gravity, and oscillations with damping and drivers. Classical Mechanics/Math Methods 2 continues with Lagrangian and Hamiltonian formalism, rigid body rotation, normal modes, orbits, non-inertial frames, linear algebra and matrix methods, and calculus of variations.
The Classical Mechanics 1 course was developed through the Science Education Initiative starting in 2009 with work from S. Pollock, S. Chasteen, R. Pepper, A. Marino, D. Caballero and many others.
The course was updated by S. Pollock and E. Neil with additional in-class tutorials and lecture notes in 2022. The Classical Mechanics 2 course was developed by several faculty at CU who shared their materials, especially E. Neil, and is not associated with any education research projects.
For details about either semester, click on the appropriate course link above.
E&M at CU is a two-semester sequence of junior-level classical electricity and magnetism.
Content coverage follows the textbook of Griffiths, Introduction to Electrodynamics)
E&M 1 covers electro- and magnetostatics, roughly Ch 1-6 of Griffiths.
E&M 2 covers electrodynamics, roughly Ch 7-12 of Griffiths.
For details about either semester, click on the appropriate course link above.
Reformed course materials were developed through the Science Education Initiative starting in 2007 with work from S. Pollock, S. Chasteen, M. Dubson, C. Baily, X. Ryan and many others.
Quantum Mechanics 1 is the first semester of our two-semester sequence of quantum mechanics.
- The box above labeled "Wavefunctions first" (above left) takes you to a research-based (CU-SEI) materials collection for a course that follows the first half of Griffiths' textbook.
- "Spins first" above takes you to a materials collection for our more recent approach, which follows McIntyre's textbook and spans two semesters.
- "Quantum Information Science" opens a separate PhysPort site
This tab contains links to materials for a variety of (mostly) undergraduate courses offered at CU Boulder.
Materials in this page are not "research-validated", they did not arise from the Science Education Initiative. They are a collection of informal materials that might prove useful if you are teaching a student-centered large University-level course.
Use what you like - give credit to sources when feasible. We ask that you do not use our materials for commercial purposes. We also ask for your cooperation in not making any solutions you may create for the homework (and exam problems, clicker questions, etc…) available on the open web, out of respect for instructors and students at other institutions, and for maintaining the integrity of our research.
Our material sets include concept tests and lecture notes, and sometimes more (e.g. course goals, etc) Courses are identified by topic, with details in each tab.
 Physics I clicker questions, exams, and lecture notes
Physics I clicker questions, exams, and lecture notes
We teach a variety of introductory courses at CU. The calculus-based sequence (Phys 1110, largely engineers) serves over 1000 students/semester, split into sections of 300 (3x 50 minutes/week), and recitations (1x 50 minutes of UW Tutorials) of 28 students. A very similar course for our majors serves (Phys 1115) about 125 students/year, same format.
The main Physics 1 download is from a recent implementation of the major's course.
Materials should still be useful for any calculus-based course (and with modification, an algebra-based course, as we don't require Calculus as a prerequisite, so we use minimal amounts of it)
These materials are research-informed but not research-validated. Primary contributors are S. Pollock, M. Dubson, and D. Bolton, with contributions from many others.
 Download_instructions_Phys1
Download_instructions_Phys1 
 Physics II clicker questions, exams, and lecture notes
Physics II clicker questions, exams, and lecture notes
Physics 2 is Electricity and Magnetism.
We teach a variety of introductory E&M courses courses at CU. The calculus-based sequence (Phys 1120, largely for engineers) serves just under 1000 students/semester, split into sections of ~300 (3x 50 minutes/week), and recitations (1x 50 minutes of UW Tutorials) of 28 students. A very similar course (Phys 1125) for our majors serves about 125 students/year, same format.
We have an (old) collection of materials from an implementation in 2007, working on some updates.
Still coming - please check back (or contact steven.pollock (at) colorado.edu if you are in a hurry!)
These materials are research-informed but not research-validated. Primary contributors are S. Pollock, M. Dubson, and D. Bolton, with contributions from many others.
 Teaching and Learning Physics
Teaching and Learning Physics
Materials from a graduate level course at CUB on Physics Education Research (cross-listed for advance undergraduates) Designed by Noah Finkelstein. The course has been taught for over 20 years at CU Boulder, typically as a small-ish (10-30+ students) seminar style course. A formal prerequisite is to have completed the standard first 2 years of undergraduate physics content courses (though exceptions can be made, but basic physics content understanding is implicitly understood)
Summary for students: A course on how people learn and understand key concepts in physics. Readings in physics, physics education research, education, psychology and cognitive science, plus opportunities for teaching and evaluating college and K-12 students. Useful for all students, especially for those interested in physics, teaching and education research. The class will largely depend upon student input.
 Introduction_and_objectives
Introduction_and_objectives AB_Course_schedule_Sp23
AB_Course_schedule_Sp23 Download_instructions_TeachingandLearning
Download_instructions_TeachingandLearning 
 Light and Color
Light and Color
We teach an interactive large-lecture course called "Light and Color" to about 100 students/term, mostly non-science majors. The course is an introduction to the science of optics, with no prerequisites (and very light on math or formalism). It uses a variety of readings, including from a (free) OpenStax textbook (College Physics 2e).
Downloads below are from a recent implementation taught by B. Wilcox.
The materials are (largely) not research-validated, but were inspired in part by earlier course transformations at CU Boulder from 2010-2017 taught by Stephanie Chasteen, CharlesRogers, Katie Hinko, and Cindy Regal, with contributions from other instructors.
 Materials_readme
Materials_readme Syllabus_CUB
Syllabus_CUB Learning_goals
Learning_goals Download_instructions_Light_color_BW
Download_instructions_Light_color_BW 
 Sound and Music
Sound and Music
This course is a large introductory level class aimed at non-science majors. The materials shared here are not research-based in any way, just some materials from when S. Pollock taught the course in 2007.
 Sound_music_readme
Sound_music_readme Sound_and_music_course_goals
Sound_and_music_course_goals Sound_and_music_materials
Sound_and_music_materials 
 Thermal Physics and Statistical Mechanics
Thermal Physics and Statistical Mechanics
We teach a senior-level thermodynamics and statistical mechanics course for physics majors, following the textbook "Introduction to Thermal Physics," by Daniel Schroeder.
Materials are not research-validated, merely shared by faculty at CU including Michael Dubson, M. Hermele, V. Gurarie, and most recently Bethany Wilcox (whose latest version is featured in the download) The course has interactive elements (clicker questions, and in-class Tutorials) developed by various faculty.
 Sample_syllabus
Sample_syllabus Material_overview_thermo
Material_overview_thermo Download_instructions_Thermo
Download_instructions_Thermo 
A sample syllabus from a recent implementation of our senior level Thermo and Stat mech course
❮
 ❯
❯
This is the second semester in our two-semester sequence of junior-level classical electromagnetism courses for physics majors, electrodynamics. Content coverage follows Ch 7-12 of Griffiths, Introduction to Electrodynamics). This includes time-dependence in Maxwell's equations, AC circuits, conservation laws, EM waves in vacuum and media, potentials and gauge transformations, radiation, and special relativity.
 E&M 2: MATERIALS DOWNLOAD
E&M 2: MATERIALS DOWNLOAD
Requests when using and sharing:
On this site, you will find a number of materials we have borrowed or developed. Feel free to use what you like - we would like to share our materials, but also believe in giving credit to sources whenever possible (and ask that you do not use our materials for commercial purposes). We ask for your cooperation in not making any solutions you may create for the homework (and exam problems, clicker questions, etc…) available on the open web, out of respect for instructors and students at other institutions, and for maintaining the integrity of our research.
 Course User's Guide
Course User's Guide Course Learning Goals
Course Learning Goals Download_instructions_EM2.pdf
Download_instructions_EM2.pdf 
See C. Baily, M. Dubson and S. Pollock, "Research-Based Course Materials and Assessments for Upper-Division Electrodynamics (E&M 2)" PERC proceedings 2012 for more early development information.
 E&M 2: Research-Based Assessment: CURrENT
E&M 2: Research-Based Assessment: CURrENT
Colorado UppeR-division ElectrodyNamics Test (CURrENT) assesses basic topics from junior-level electrodynamics, where the focus is on gauging student understanding of fundamental concepts, and whether they can complete basic advanced E&M tasks. The topic coverage in this assessment is limited to core material that is likely to be taught at most institutions, since we’ve found there to be some variance due to institutional peculiarities. There is also a short pre-test on a more limited set of questions. You can learn more and download the the open-ended version (with scoring rubrics) from PhysPort using the link above.
Online, multiple-response versions of both pre- and post-tests are under development, with a beta version implemented on Qualtrics. Contact Steven.Pollock (at) Colorado.edu if you would like to try this in your class.
 E&M 2: About the Course
E&M 2: About the Course
E&M 2 is the second semester of our junior-level classical electromagnetism sequence. We have compiled a number of resources which can be easily incorporated into a standard university class structure. These resources were designed to encourage students to be active participants in the learning process. See the Materials tab for all materials in one download.
Here, we briefly summarize our transformations with tips to implement them yourself.
The primary text we used for this course is D.J. Griffith, Introduction to Electrodynamics (Prentice-Hall, Upper-Saddle River NJ, 1999) [Ch. 7-12]).
The following additional textbooks were recommended by electrodynamics instructors at CU Boulder, and various physics faculty at outside institutions:
- G.L. Pollack and D.R. Stump. Electromagnetism (Addison Wesley, San Francisco, 2002). A more mathematical text, including some material on numerical relaxation techniques. Several more problems worked out in text than Griffiths, and a more thorough coverage of currents, magnetostatics, induction and EM waves.
- J.R. Reitz, F.J. Milford, R.W. Christy. Foundations of Electromagnetic Theory, 4th Ed. (Addison Wesley, Menlo Park, 1993). Nice chapters on microscopic pictures for polarization and magnetization, on plasmas, and on superconductors.
- J.D. Jackson, Classical Electrodynamics, 3rd edition (Academic Press, New York, 1998). The graduate textbook, this is beyond what is accessible to most students in this course.
- R.P. Feynman, R.B. Leighton, M. Sands. The Feynman Lectures on Physics, Volume II (Addison-Wesley, Reading Massachusetts, 1964). Still a classic, this volume has some extremely illuminating sections on E&M, including real-world examples and conceptualizations of the equations.
- R. Chabay and B. Sherwood, Electric and Magnetic Interactions (John Wiley & Sons, New York, 1995). This introductory level textbook has a wealth of real-world examples of E&M.
- E.M. Purcell, Electricity and Magnetism: Berkeley Physics Course Vol 2 (McGraw Hill, New York, 1985). A sophomore level introduction to E&M, well-written and easily followed.
- A. Shadowitz, The Electromagnetic Field (Dover Publications, New York, 1975). A well-written text which includes solutions for odd-numbered problems and many worked examples. Has a slightly more engineering bent than most physics texts.
The bulk of the material in this course is fairly canonical across universities. At the University of Colorado, the content coverage and order closely follows chapters 7-12 of Griffith's text.
We begin with an introduction to electrodynamics (EMF, Faraday, Maxwell's equations with time dependence), add a practical unit on inductors in circuits, then move to conservation laws, Poynting vector and the stress tensor, then EM waves, time-dependent potentials and fields, radiation, and end with special relativity.
Additional commentary on the presentation of certain topics can be found in the Materials download tab.
Our course requires that students have passed E&M 1 (electro- and magnetostatics) before starting the second semester. Mathematical expectations are no different than for E&M: 3 semesters of calculus, plus differential equations. Faculty may choose give a content pretest to students to both (a) assess where students are weak, and (b) send students the message that this is material they should already be familiar with.
There is a general consensus among faculty that the bulk of the learning in this course comes from doing the homework. This course is where students learn a certain level of sophistication in solving problems (see Learning Goals tab). Homework should reflect that higher expectation. We have compiled a homework bank of useful problems designed to target these higher level goals. Additional ideas for creating homework sets can be found in the Course User's Guide. Some were written by CU faculty, but many were also borrowed and adapted from others (including textbooks), modified to emphasize sense making and/or connections to real-world situations.
We ask for your cooperation in not making solutions to these homework questions available on the open web.
These were given at the very beginning (as in, the first day), turned in on the second day of class. In the end, both ways of doing it provided a great deal of information about what students were capable of after a long break between semesters, and helped us decide how to approach the first week of the semester, which was devoted to review topics from electrostatics.
See the Materials download, where our homeworks are available in Word and pdf versions from several semesters. (Feel free to adapt, alter, and improve. Do try to significantly change our wording, and do not post CU solutions, thanks.)
Preflights are short questions or tasks asked online, used to orient students to upcoming material. They are meant to encourage reading the textbook before coming to class, and to reflect on key points in the material. Responses can be used by an instructor to inform their preparations for upcoming lectures, by focusing on specific difficulties students have with new material.
These preflights were loosely modeled on ones from the US Air Force Academy, an upper-division offshoot of Just-in-time Teaching (JITT). For more information, see: G.M. Novak, E.T. Patterson, A.D. Gavrin and W. Christian, Just-in-time Teaching (Prentice-Hall, Englewood Cliffs NJ, 1999), and other publications associated with these authors.
Our preflight assignments were due several hours before class early in the week. They represented a small percentage of their total grade, and were graded strictly pass/fail, based effort and not correctness. Preflights at CU were administered online, but the Materials download contains screenshots or pdf versions.
Comment: Preflights were not particularly popular with our students, though they were extremely useful to us as instructors and education researchers. In other words, despite the valuable information we received from students, they did not claim to find the preflights particularly helpful for their learning (only 14% of SP12 and 30% of FA11 students rated preflights as either useful or very useful for their learning). This may in part be due to low student participation (they needed constant reminders in both courses that the preflights were due each week), and many students reported being averse to doing work over the weekend. In later courses we have found that discussing student responses in class, responding individually to some every week, and promoting their value go a long way in improving student attitudes.
In lieu of “office hours” in a faculty office, our courses hold twice-weekly homework study (or "help") sessions outside of class. We devote 1-2 hours each session, timed to be convenient to a large fraction of the class (based on polling), the 2 days before homeworks are due. Learning assistants or TAs can staff these sessions if you have them available. Our sessions were held in a large room with sufficient table space for students to work together on the homework problems, with occasional guidance from an instructor. This was particularly enlightening to us as instructors and researchers, since we could observe students as they were engaged with the work. They were also extremely popular with students (84% of students who came rated these sessions as useful or very useful for their learning.) Attendance was typically ~1/3 of the class, we found it important to remind students and strongly encourage them to come.
There are a variety of lecture techniques that have been shown to be useful in student engagement.
1. Clicker questions
Clickers are wireless personal response systems that can be used in a classroom to anonymously and rapidly collect an answer to a question (usually multiple-choice) from every student. This allows rapid reliable feedback to both the instructor and the students. Alternatively, clicker questions can still be used without the personal response system by using colored cards or hand signals. See the Colorado Science Education Initiative website for additional information and resources for effective use of clicker questions.
Many consider Richard Hake’s 1998 AJP paper a wake-up call for physics instructors, demonstrating that traditional teaching methods (lectures with occasional demonstrations) are largely ineffective in fostering a deep understanding of physics. Hake analyzed introductory physics courses across institutions (See Ref 1 below), categorizing them as traditional or incorporating active engagement techniques. Students completed the Force Concept Inventory (FCI) pre- and post-instruction, testing mastery of Newton’s laws. Results were measured by learning gain <g>, which compares how much students learned to how much they had yet to learn at the start. This relative measure accounts for variations in students’ prior knowledge, enabling cross-institutional comparisons of instructional effectiveness.
Traditional lecture courses showed consistently low learning gains, typically in the 20–30% range—indicating students learned only about one-quarter of what they didn’t already know. While some active engagement courses also had low gains, the majority achieved two to three times higher learning gains than traditional ones. These findings have been replicated in other studies (Ref 2 and 3 below), which also show that interactive tutorials improve long-term retention of conceptual understanding in E&M compared to traditional recitations. These results highlight that while active engagement is critical for learning, how it is implemented matters.
Active engagement is rarely applied to upper-division courses, despite evidence supporting its effectiveness at the introductory level. Pollock (Ref 4) compared pre- and post-instruction scores of junior-level electromagnetism students on the Brief Electricity and Magnetism Assessment (BEMA), a measure of fundamental concepts from introductory E&M. He found no significant improvement in scores after traditional advanced E&M instruction, suggesting that the teaching approach did not help solidify students’ grasp of foundational concepts. This raises concerns about whether students can develop a deep understanding of more advanced topics without mastering the basics.
If active engagement benefits introductory courses, why not apply it to advanced ones? Instructors often view upper-division courses as fundamentally different. The topics are more abstract and mathematically formal, and students have already demonstrated aptitude by progressing to this level. Smaller class sizes allow for more interaction, and instructors often see these courses as preparation for graduate study. Many faculty teach upper-division courses as they themselves were taught, believing the nature of the material requires a more traditional approach.
However, research shows many advanced students are not learning as effectively as we hope (Ref 5). Active engagement, such as clicker questions, provides opportunities for students to recognize gaps in understanding and apply concepts in real-time. Even in small classrooms, students often do not realize they are confused or know what questions to ask without structured prompts. Clicker questions also help instructors gauge comprehension during lectures. Active engagement fosters scientific argumentation—an essential skill developed through practice as students articulate and defend their understanding.
Student response to active engagement in upper-division courses has been overwhelmingly positive at CUB. Surveys at CU found that 80% of students who experienced clicker questions in advanced courses felt they enhanced their learning compared to lectures alone, with around 15% neutral. Few believed clickers detracted from their learning experience. This feedback underscores the potential of active engagement to improve advanced instruction, building on its proven success at the introductory level.
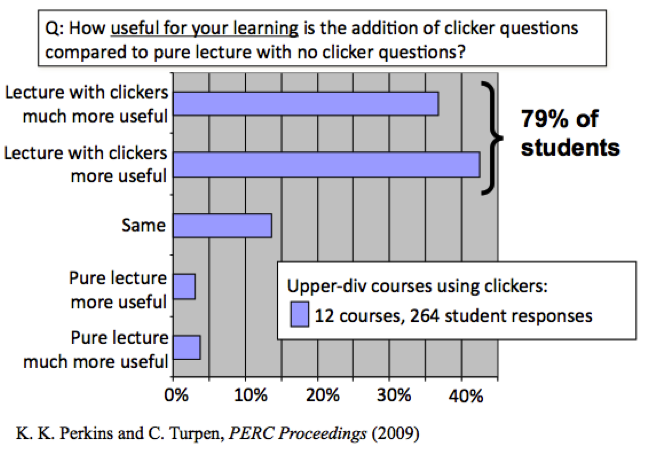
Just as interesting is the fact that, as with many instructors, students who had never used clickers in an upper-division course were skeptical about their usefulness in that context. Students were asked following a popular pure-lecture course on quantum mechanics if they would recommend using clickers in advanced courses, with the majority responding either neutrally or not recommending their use.
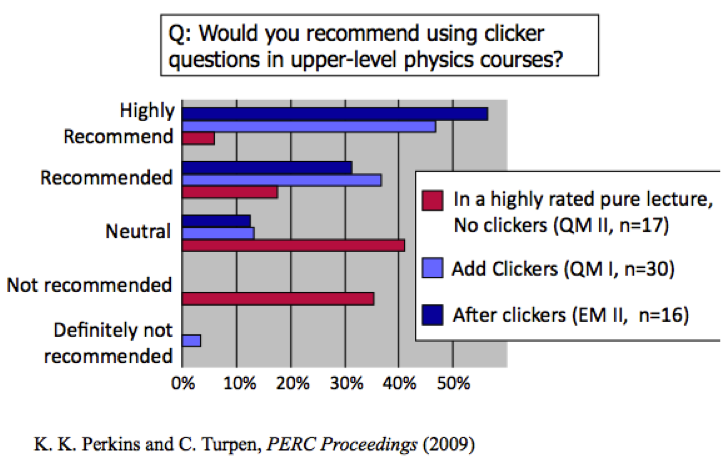
In contrast, most students from a quantum mechanics course that had used clickers during lecture would recommend using them in advanced courses. Students who had used clickers in a first-semester electromagnetism course continued to favor their use after taking the second-semester course (E&M II), where they were not used.
Having motivated the use of clicker questions in upper-division courses, a natural question is: how can they be effectively incorporated into lectures? Active engagement doesn’t require instructors to give up lecturing entirely, and clicker questions can be judiciously inserted into a lecture at key points for a number of purposes, for example: to check for conceptual understanding, to have students apply a concept to a new situation, to underscore an important idea in a long derivation, or to help them make connections between a physical system and the mathematics used to describe it. Specific examples of these are given below.
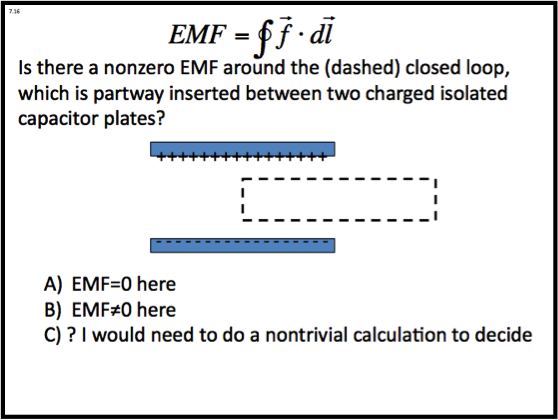
Clicker questions are often only associated with testing conceptual understanding – asking students to come up with an answer without resorting to mathematical calculations. The sample question below asks whether the electrostatic field of a charged capacitor plate is capable of generating a non-zero EMF around a closed loop. This question was used in two separate electrodynamics courses at CU, and in both cases ~25% of students got this wrong; when asked, many of them intuitively knew that a charged capacitor shouldn’t be able to drive a current around a loop, but some weren’t considering the existence of fringing fields, or couldn’t visualize how they were causing the line integral to vanish.
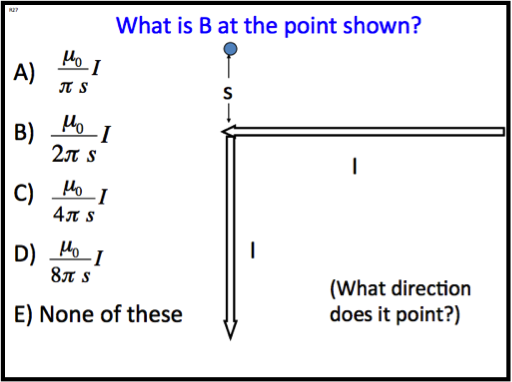
Students can also test their understanding of important concepts by applying newly derived results to a novel situation. In one of our classes, following a standard derivation of the magnetic field due to a long, straight wire using Ampere’s law, students were asked in the following question about the magnetic field at a point near a long wire that takes a 90 degree turn. Answering this question requires students to consider the role of symmetry in deriving the answer for the straight wire, and also the directional variation in the field produced by a section of current according to the Biot-Savart law. Because the vertical section contributes nothing to the field at point s, the field can be found by simply dividing the expression for a straight wire by half. Most students initially got this question wrong.
Sometimes there is an essential point that students must keep in mind in order to follow along with an important derivation. When discussing Maxwell’s modification to Ampere’s law, arguments involving the continuity equation required students to know that the divergence of the curl of a field is identically zero. The question below was used to underscore the importance of this point in the derivation, and to be sure that students realized this was a general result, and not specific to any particular type of field.
Clicker questions can also be used to help students make a connection between a physical situation and the mathematics used to describe it. A mathematical formula for the electric field is required to answer the question below, which essentially asks them to relate the curl of an electric field to the rate of change of magnetic flux in that region. Even though the field may appear “curly” to students, the 1/distance dependence of the field actually makes its curl everywhere zero except at the origin. This answer can be gotten without looking at the explicit expression for the curl of a field in cylindrical coordinates, by using a specific line-integral as an example, where the increase in arc length along a curve at a greater distance from the origin exactly cancels the diminished magnitude of the field. Before discussion, students in the FA11 and SP12 E&M II classes at CU were evenly split between the curl being zero (A) and non-zero (B).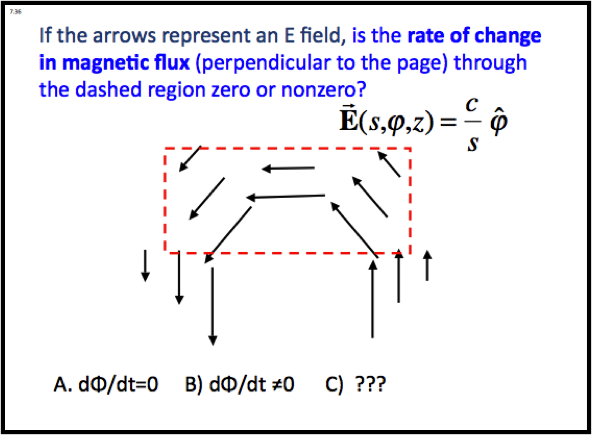
- R. Hake, …A six-thousand-student survey…, Amer. J. Phys. 66, 64-74 (1998).
- S. Pollock and N. Finkelstein, Sustaining Educational Reforms in Introductory Physics, PRST-PER 4, 010110 (2008).
- S. Pollock, Longitudinal study of student conceptual understanding in electricity and magnetism, PRST-PER 5, 020110 (2009).
- R. E. Pepper, S. V. Chasteen, S. J. Pollock & K. K. Perkins, Observations on student difficulties with mathematics in upper-division electricity and magnetism, PRST-PER 8, 010111 (2012);
- R.E. Pepper et al, "Our best juniors still struggle with Gauss’s Law: Characterizing their difficulties", PERC Proceedings 2010, AIP Press (2010).
- K. K. Perkins and C. Turpen, Student Perspectives on Using Clickers in Upper-division Physics Courses, PERC Proceedings 2009, AIP Press (2009)
Clicker questions (with notes and comments) are all available from our Materials download tab.
2. Interactive lecture
When solving a problem on the board, the lecturer can pause and ask the class for the next step. If the course culture has included the use of clicker questions, so that students are habituated to actually engaging with this sort of question (instead of waiting for the smartest student to answer), then this type of discussion can occur without the use of actual clickers in every instance. The class should be given a time limit (e.g., “You have 30 seconds; write down your answer”) to focus their discussion. We find that students are more likely to actually write something down on paper if the lecturer leaves the front of the room and talks briefly to students in the middle of the room.
3. Class discussions
In addition to clicker questions, faculty can pose open-ended questions (non multiple choice) for discussion in class, providing students an opportunity to engage with the concepts in class. The more that instructors are clearly open to discussion in class, the more students will feel comfortable posing spontaneous questions.
4. Don’t repeat examples from the text
Students can read the chapter as they work on the problem set. It may be useful to encourage students to read the chapter before lecture, if the professor does not intend to reiterate material from the book in lecture. In that case, lecture may be spent in productive discussion and engagement with the material. Students can easily read derivations and similar content in the book, and so professors may decide how much of that content should be included in lecture.
5. Whiteboard or Chalkboard Activities
We have successfully used whiteboards and student work at the blackboard in class and out of class. Large (2x3 foot) whiteboards provide a convenient public work space for group activities. Small (1x1 foot) whiteboards work well for individual or partner work while still allowing instructor to quickly see what students are getting in a lecture (by walking around to individual whiteboards or by asking students to “publish” their results by holding up their whiteboards).
Additional information on some of the advantages and disadvantages to whiteboard activities can be found in the Course User's Guide or you can browse our in-class activities for specific examples.
5. Tutorials
Tutorials are conceptually focused worksheet activities designed to be done in small groups and target known student difficulties. They are designed to be completed in a 50 min co-seminar; however, some instructors at CU have incorporated Tutorials into lecture. See the next section below for many more details (including how to run them, what topics are available, and some instructor guides with timing suggestions for each one)
6. Help-sessions
In the reformed course, we encouraged students to work in small groups on the homework. They learn by peer instruction with occasional input from the instructor, as in the tutorials. Each group may have a group-sized whiteboard (see above), and the staff present do not work out problems on the board. We try to offer two homework help sessions – two nights and one night before the homework is due.
Use the Materials tab to find Tutorial source files.
Our guiding principle in creating these activities was that students would gain more from being active (instead of passive) participants in the classroom. The tasks are focused on promoting understanding of important topics from second-semester E&M, and/or guiding students through derivations that would typically be done during lecture. Many were inspired by in-class observations of student difficulties, and have been tested in focus-groups and in the classroom.
We ask for your cooperation in not making solutions to these tutorials/activities available on the open web under any circumstances - additional reasons for this (beyond the obvious) are addressed in the implementation notes (Section I, below).
A short (4-page) paper on the process of developing these tutorials: "Developing Tutorials for Advanced Physics Students: Processes and Lessons Learned", Charles Baily, Michael Dubson and Steven J. Pollock PERC Proceedings 2013 pdf
These tutorials/activities were developed for use during class, to augment or replace standard lectures on the topics they address. This style of implementation is in contrast to introductory-level Tutorial settings, being separate from the lecture portion of the class, but they could certainly be adapted for use in such environments, and we encourage instructors to do so.
Depending on the topic, they require anywhere from 10 to 50 minutes of class time, and versions of them were recently used intermittently during a course having 50-minute class periods (three times per week over a 15-week semester). ~40% of CU SP12 lectures included tutorial activities. We encourage you to personalize the materials, including shortening them considerably (Over time, we are finding that limiting Tutorials to just one page front and back makes a good length)
We orient students to the activities before they began with a concept test and/or discussion. They are implemented at appropriate times during lecture, often during the middle, sometimes at the end of class.
Incorporating these student-centered tasks into the classroom was sometimes challenging, and we describe below some lessons we have learned about getting the most out of the time spent.
(1) Sell students on group work. Students will have their own ideas about what a junior-level physics classroom should be like, and some may at first be reluctant to engage in activities that differ from the standard lecture format (even when they are familiar with them from introductory courses, and particularly if they associate them only with “lower-level” work). Aside from the belief that they will gain more through active participation, instructors may also remind students that scientific argumentation (oral or written) is a skill that is developed with practice, and that scientists work almost exclusively in group settings. Stronger students benefit from working with weaker students (and not just the other way around) since, as we should know from our own teaching experiences, they will never understand something so well as when they can explain it to someone else!
(2) Hand out just before activity begins. We’ve found that handing out the printed activities at the beginning of class (or a significant amount of time before starting them) is not ideal. There will inevitably be some students who immediately start reading through the pages or working the problems, and mostly tune out the instructor from that point on, so instructors should be aware they might not have the undivided attention of the class once the activity sheets are in front of students. This can also discourage students from collaborating with others at their table, since they’ll be ahead of everyone else and may be reluctant to go back.
(3) Keep it closed note. We have tried to provide students with sufficient information to complete these activities without having to refer to their notes. Some of the tasks do require them to recall facts from memory, but this is only in cases where we feel they should have this knowledge at their fingertips, and instructors can certainly write out necessary equations on the board if they wish. If there are instances where students feel they must refer to outside sources, this should be an indication to them that they may need to devote a little more time to studying that particular topic. We actively discouraged them from copying equations or following examples from the textbook, since this does not involve the kind of understanding we are trying to promote.
(4) Introduce the activities. Students may require some kind of orientation to the topic at hand, or need an important piece of information to get started; they may also need you to be explicit in connecting the tasks as a whole to your overall learning goals. We have tried to be as clear as possible in the problem statements, and their wording has (in most cases) already been tested with students, but what seems “obvious” to instructors may not be so for students. We have also noticed that, even at the junior-level, some students don’t always read each problem statement completely, often only skimming the words and trying to glean as much information as possible from the diagrams.
(5) Activities may take longer than anticipated. All of the activities (except where explicitly noted) have been validated through student interviews and field-tested in a classroom setting. The summary that accompanies each tutorial has an estimate of the amount of time it should take for most students to complete the entire activity, but an actual implementation may take more (or less) time than anticipated. We notice there is a tendency for instructors to underestimate the amount of time it will take students to complete these activities; a general rule is that students usually take around 10 minutes per page.
(6) Use challenge problems, or create new ones. When students are working at their own pace, there will always be groups who are much quicker than others to complete the tasks. To keep these students using their time productively, many of the activities have one or two challenge questions at the end, which usually involve taking their conclusions a step further. If there isn’t a challenge question, instructors should be prepared with a question or task for students that builds in some way off of the tasks they’ve just completed.
(7) Don’t provide written solutions. There have been studies that suggest students will learn and retain more when they are not given written solutions to tutorials, though it is essential that tutorial instructors ensure that students are arriving at correct answers as they progress through the tasks. Some students may feel frustrated by this policy, but we suspect that referring to an answer key while studying may short circuit an important aspect of the learning process, namely arriving at a correct answer through their own reasoning, and being able to justify the correctness of that answer. For our class, activities were posted on a secure site for students who were unable to attend, and we encouraged them to speak with us (and each other) outside of class about any questions they might have. Most importantly, they should ask questions during class time, when they recognize that they’re confused. We do ask that you not post solutions to these activities on the open web under any circumstances, out of respect for instructors at other institutions, and for maintaining the integrity of our research.
The ordering of topics for these activities follows the presentation in Griffiths (except for AC circuits, which is sparsely covered in his book). The activities are usually sufficiently self-contained that they can be used independent of each other, but they sometimes come in two parts, or use language we expect students to be familiar with from earlier tasks. We make note of this in instructor notes when applicable.
The general topics covered in each of the tutorials/activities are listed below, along with the estimated time it will take for most students to complete them.
| 00 - Review Material | |
| A - Divergence & Stokes Theorems | ~ 15 min. |
| B - Gauss' Law | ~ 15 min. |
| C - Ampere's Law | ~ 15 min. |
01 - Current Density |
~ 15 min. |
02 - Ohm's Law |
< 50 min. |
03 - Faraday's Law |
< 30 min. |
04 - Complex Exponentials |
< 50 min. |
05 - Complex Impedance |
< 50 min. |
06 - Maxwell-Ampere Law |
|
| A - Part 1 | ~ 25 min. |
| B - Part 2 | ~ 25 min. |
07 - Boundary Conditions |
< 50 min. |
08 - Energy Flow in a Simple Circuit |
< 40 min. |
09 - Linear Operators |
< 15 min. |
10 - EM Wave Equation |
~ 10 min. |
11 - Complex Plane Waves |
< 40 min. |
12 - Reflection & Transmission |
|
| A - Normal Incidence | < 50 min. |
| B - Oblique Incidence | ~ 30 min. |
13 - Gauge Invariance |
< 50 min. |
14 - Retarded Potentials |
~ 30 min. |
15 - Special Relativity |
|
| A - Length Contraction | < 15 min. |
| B - Inelastic Collision | ~ 10 min. |
| C - Velocity Transformation | ~ 10 min. |
00 – Review Material
These are meant to be short review activities, so the time-estimates are based on students already having a reasonable familiarity with these topics from the first semester of the course.
0A – Divergence and Stokes’ Theorems (~15 minutes)
Topics: Divergence theorem, Stokes’ theorem, Gauss’ law, Ampere’s law.
Summary: Students are asked to state the divergence theorem and Stokes’ theorem, and then work backwards from the integral forms of Gauss’ law and Ampere’s law to derive these expressions in differential form.
Comments: Many students will have difficulty recalling these two mathematical theorems from memory, but we encourage them to do this because perpetually copying out of a book does not demonstrate understanding, and we also believe that writing them down should be straightforward if they genuinely understand what they mean. Students are typically asked to derive the integral forms from the differential forms, and these tasks have them do it in the other direction. The greatest difficulty for them was in justifying dropping the integration symbols in the final step of their derivations; students may recognize that two integrals being equal doesn’t necessarily mean the integrands are equal, yet still make the mistake of implicitly assuming this.
0B – Gauss’ Law (~15 minutes)
Topics: Gauss’ law, symmetries, electric field from a line charge distribution.
Summary: Students consider the symmetry of a line charge distribution to argue for why the electric field is entirely in the radial direction, and why a Gaussian cylinder is needed to solve for the electric field (instead of a sphere or a cube). Students are then asked to recall Gauss’ law in integral form, find the charge contained in a section of wire, and solve for the electric field.
Comments: Many students had difficulty articulating their reasoning on the symmetry questions, and were more inclined to argue in terms of the curl (or closed line integral) of an electrostatic field being zero. A significant number of students will believe that the electric field can be solved for using Gauss’ law and a non-symmetric surface, but that we don’t use such surfaces because the integral would be too difficult to calculate. All of this indicates that students may have the rote application of Gauss’ law down, without necessarily having a strong grasp of the important role of symmetry when calculating fields.
0C – Ampere’s Law (~15 minutes)
Topics: Ampere’s law, symmetries, magnetic field of a long wire.
Summary: Students first argue for why the magnetic field is entirely in the tangential direction for a straight current-carrying wire. They are then asked to recall Ampere’s law in integral form, and solve for the magnetic field around the wire.
Comments: The previous activity on Gauss’ law was more explicit about making symmetry arguments, and many students may still do this after having completed that prior activity. Others were more comfortable thinking in terms of there being no magnetic charges, and the curl (or closed line-integral) of the B-field being zero where there is no current (enclosed). Instructors should be aware that understanding the symmetry arguments in applying Gauss’ law doesn’t necessarily translate to the context of Ampere’s law. A challenge question at the end asks if Ampere’s law can be used to find the B-field at the center of a circular loop of current, which inspired a great deal of good discussion/questions.
01 – Current Density & Charge Conservation (~15 minutes)Topics: Current density, conservation of charge (continuity equation).
Summary: Students first consider a cylindrically symmetric conductor having three regions of different cross-sectional area. The task here is to rank order the three regions in terms of several physical quantities in those regions: conductivity, total current, current density and electric field. The remaining tasks connect the flux of the current density through a closed surface to the rate of change of the charge enclosed within the volume.
Comments: These tasks were overall relatively straightforward for students. A common difficulty that arose had to do with whether the outward flow of current corresponding to positive flux, and if (- dp/dt) is a positive quantity. A challenge question at the end has them convert the integral form of the continuity equation to its differential form.
02 – Ohm’s Law (< 50 minutes)
Topics: Ohm’s law, continuity equation, boundary conditions on the electric field inside a conductor
Summary: A steady current flowing through a cone-shaped resistor is used as the context for addressing the implications of the microscopic version of Ohm’s Law (J = σE). The initial multiple-choice question orients students to the situation by having them consider the current density inside the resistive material. They are then led to make conclusions about the electric field and local charge density inside the resistor by using Ohm’s law in conjunction with the continuity equation and Gauss’ law. Students are presented with two possible configurations for the electric field inside the conductor, and are asked to identify which aspects of those configurations are allowed, and which are precluded by boundary conditions or conservation of charge/current. The final activity asks them to interpret a graph of the correct field and equipotential lines inside the resistor in terms of the concepts discussed in the previous sections.
Comments: Instructors should be sure that students reconcile their mathematical conclusions (Div.E = 0 inside the resistor) and the fact that the field lines are spreading outwards (which may look to them like a “diverging” field). It is not essential that the field lines drawn by students on the second page are completely correct before moving on – we just want them to develop some kind of expectation for what they ought to look like.
03 – Faraday’s Law (< 30 minutes)
Topics: Faraday’s Law, fields of a solenoid with time-varying current.
Summary: Students first sketch the B-field for a long solenoid, and then consider whether there is a non-zero electric field anywhere in space when the current in the solenoid is changing with time. They then use Faraday’s law in integral form to compute the electric field inside and outside the solenoid, and sketch the induced field as a function of distance from the center.
Comments: This is a shortened version of a tutorial on EMF from a series created by the University of Colorado for the first semester of this course. The biggest conceptual difficulty for students has been with the idea that there is a non-zero electric field in a region of space where the magnetic field is zero (outside the solenoid). This can lead to good discussions on the difference between the differential and integral forms of Faraday’s law. There have been a few students who were concentrating only on the electric field driving the current in the coil, and weren’t thinking there could be an electric field anywhere but inside the wire. This can lead to interesting discussions about the relative magnitudes of the induced electric field and the field driving the current, and how this could depend on the dimensions of the solenoid or the rate of change in the current.
04 – Complex Exponentials (< 50 minutes)
Topics: Complex exponentials as oscillatory functions, representations of complex numbers, simple AC circuit with resistor.
Summary: The first tasks are meant to help students gain some familiarity with complex exponentials as oscillatory solutions to differential equations. They first consider similarities and differences between exponential and trigonometric functions as solutions to a first-order equation, then similarly for the behavior of their second-derivatives. Students then perform a few basic tasks involving different representations of numbers in the complex plane, and draw conclusions about the direction of rotation over time for an arrow representing a complex exponential function. The final task applies to a simple AC circuit, where students must find the magnitude of the current through the resistor at a specific time.
Comments: The first task may seem “simple”, but we were surprised by the amount of time that some students took to find the first-derivatives of the functions given; a sign error here and there was common. Students didn’t necessarily have problems completing the exercises on complex numbers, but seem to require more practice in order to be comfortable with them; some will be rusty on the rules for multiplying exponentials functions. Questions about a vector rotating in the complex plane are given in anticipation of their use in future tutorials (#5-Complex Impedance, #7-Boundary Conditions, and #12-Reflection and Transmission). We’ve found this to be a very powerful visualization tool for students when working with oscillatory functions. Some students have shown a tendency to confuse their use of complex exponentials in quantum mechanics (multiplying by the complex conjugate to find a physical quantity) when finding the physical voltage or current represented by a complex exponential (instead of looking at just one component).
05 – Complex Impedance (< 50 minutes)
Topics: Complex impedance, phasor diagrams, RLC circuits, leading vs. lagging
Summary: These activities are meant to help students gain facility with different representations of complex functions, and with relating them to the behavior of an RLC circuit. They begin by plotting voltage (and current) relative to a given current (or voltage), using a specific value for the complex impedance. They can compare their answers with trigonometric representations, and resolve difficulties in deciding whether one function leads or lags the other in time. Students then determine the total impedance in an RLC circuit in terms of the impedance for each circuit element, and plot various vectors in a phasor diagram to see how they are related.
Comments: Students are assumed to have either completed the previous activities on complex exponentials, or had some kind of introduction to writing complex numbers in various forms, and the multiplication of complex exponentials (frequent errors come from not being familiar enough with the rules of exponents). There has been a great deal of confusion among students concerning whether a voltage is leading or lagging the current, depending on which representation being used. It seems to be fairly intuitive for them when looking at the phasor diagrams (as long as they’re clear on the direction in which the vectors are rotating with time); but the trigonometric representations can be challenging because, in the graph of a function that is leading in time, it peaks at a point that is to the physical left of the peak for the function it leads, and therefore “looks” like it’s actually lagging.
6A – Maxwell-Ampere Law, Part 1 (~25 minutes)
Topics: Maxwell-Ampere law, conservation of charge, E- and B-fields for a charging capacitor.
Summary: After first converting the Maxwell-Ampere equation from differential to integral form, students draw conclusions about dp/dt and Div.J for a circuit with a charging capacitor, and compare them with what’s predicted by the static form of Ampere’s law. They are then asked to compare these incorrect predictions with those for the full Maxwell-Ampere equation, and consider how this is related to the continuity of field lines for a divergenceless field (the vector field Curl.B).
Comments: The other activity on this topic (Maxwell-Ampere Part 2, #6B) can also be done in approximately 25 minutes, so the two parts could potentially be used in the same class period, or just split between two classes. When deriving the Maxwell-Ampere law in integral form, 40% of our students incorrectly substituted Qencl/eps_0 for the open-surface flux integral of E (an incorrect application of Gauss’ law, where the flux integral is over a closed surface). Many students were confused about the sign of the net flux of the current density in a region where a capacitor plate is charging – usually because they were not considering the different directions the area vector points in around the Gaussian surface; many were incorrectly thinking that a net charge flowing into the volume would correspond to positive flux. About 1/4 of our students were confused by the questions regarding charge conservation, thinking they were instead asking about whether there was an equal but opposite amount of charge on the two capacitor plates. In a handful of cases, students initially believed that charge was actually flowing through the space between the capacitor plates, so that the charge flow was continuous through the circuit. Students may need to be reminded that the divergence of the curl of a vector field is always zero.
6B – Maxwell-Ampere Law, Part 2 (~25 minutes)
Topics: Maxwell-Ampere law, Gauss’ law, E- and B-fields for a charging capacitor, B-field of a current-carrying wire.
Summary: After converting the Maxwell-Ampere equation from differential to integral form, students find the magnetic field outside a current-carrying wire. They then consider the electric field between the capacitor plates in terms of the current in the wires and the charge density on the plates, and derive a formula for the magnetic field between the plates induced by the changing electric field. They can then compare the magnitude of the field outside the wire with the field between the plates, specifically for the case where the radius of the Amperian loop is such that it encloses all of the electric flux (they are then the same).
Comments: The task of converting Maxwell-Ampere from differential form to integral form is repeated because students have shown they have real difficulty in doing this without a textbook in front of them. Instructors may not want to skip this if Parts 1 & 2 are used in the same day. Many students showed continuing difficulty with choosing the correct surfaces and loops for applying the integral equations – specifically with seeing how the two types of integrals are related to each other by the same surface. An additional task for students could be to explain the final result in terms of the continuity of field lines for the divergenceless field Curl.B, which was also addressed at the end of the previous tutorial.
07 – Boundary Conditions (< 50 minutes)
Topics: Boundary conditions, Maxwell’s equations in integral form.
Summary: These activities guide students through a derivation of the boundary conditions on the electric and magnetic fields at the interface between vacuum and a general material. Initial tasks have them consider the charge/current/flux enclosed by imaginary surfaces. They are then guided to apply Maxwell’s equations to solve for the conditions on the fields at either side of the boundary.
Comments: Just prior to implementation, we gave our class a brief review of sign conventions regarding unit vectors and integration surfaces/loops. During the tasks, many students were still introducing minus signs into the equations from memory (or intuition), without being able to justify them in terms of the direction of the unit vectors. Some students are confused by the distinction between a surface current and the volume current “right at the very edge” of a material, and this is addressed by having them consider the charge/flux enclosed by surfaces with dimensions that shrink to zero, in this case just across the surface. Some students got very caught up on whether the charge/current/flux enclosed is actually zero, or just vanishingly small – this can be an opportunity to discuss comparisons between finite quantities and ones that are differentially small. We have purposefully avoided reference to the auxiliary fields D & H, and there is no distinguishing here between free and bound charges/currents, because of the added complexity this would involve.
08 – Energy Flow in a Simple Circuit (< 40 minutes)
Topics: Poynting vector, boundary conditions, surface charges, Ohm’s law
Summary: These activities focus on the location and direction of energy flow for a circuit containing just a battery and a resistor; the initial tasks consider only a resistive element with a current flowing through it. Students should first conclude that energy is flowing radially into the resistor (and not along the direction of current), and that Faraday’s Law requires the electric field to be nonzero outside the resistor. With no volume charge density inside the resistor, the next conclusion is that surface charges are responsible for the perpendicular components of the electric field, which must vary along the length of the resistor for the field to be conservative. The final conclusion is that energy flows from battery to resistor through the fields outside the conducting wires, and that energy can (counter-intuitively) flow opposite the direction of current.
Comments: The part concerning the parallel components of the electric field outside the resistor may be more challenging for students who did not complete the tutorial on boundary conditions. There were still a few students who believed the volume charge density inside the resistor is non-zero (even though the current is steady), so this activity gives another opportunity to address this (see #2-Ohm’s Law). The final conclusion about the location and direction of energy flow was surprising to most students, and instructors should be sure that students don’t automatically assume the direction of energy flow is the same through the entire circuit (from positive to negative terminal, instead of outwards from both). Many students strongly associate the Poynting vector only with electromagnetic waves, so this activity provides another context for them.
09 – Linear Operators (< 15 minutes)
Topics: Linear differential operators/equations
Summary: Linear operators are defined, and students must determine which of five operators are linear. The second part addresses how the components of a complex solution are themselves solutions to a linear differential equation.
Comments: Students should be sure to check their answers to the first part, since many will mistakenly believe that option IV is linear if they don’t think too hard about it. The final task is designed to address potential confusion about how to translate between complex exponential representations and physical solutions.
| PDF Word | Back to list |
10 – EM Wave Equation (~10 minutes)
Topics: Wave equation, Maxwell’s equations.
Summary: This is a mostly mathematical exercise, to have students derive the wave equation for the electric field in a vacuum (where there are no charges or currents).
Comments: The initial task of deriving the wave equation should be completed within 5-10 minutes, though some may need help in getting started. The final part asking about static fields has been added since the implementation in our class, but we expect that there will be some students who are confused about whether this statement about fields in a vacuum is general. The biggest confusion we’ve seen for students is how the wave equation for EM fields is usually written as a compact vector equation, where it can look as though the Laplacian is operating on the entire vector, instead of each of its components separately.
11 – Complex Plane Waves (< 40 minutes)
Topics: Plane waves, complex exponentials
Summary: The initial tasks have students identifying the various quantities that go into a plane wave represented by a complex exponential; the first involves constructing an expression from the quantities given, while the second analyzes the quantities for an expression that’s given to them. The remaining tasks involve deriving explicit expressions for the divergence and curl of a plane wave, and relating them to Maxwell’s equations in vacuum to determine the orientations of the electric and magnetic fields relative to the direction of propagation.
Comments: We’ve noticed that students can have trouble parsing out the various vectors and scalar quantities that go into a plane wave expressed in complex exponential notation; the first two tasks give them practice with this. When taking partial derivatives of the complex exponential, many students had difficulty correctly applying the chain rule; in particular, they often didn’t see that the dot-product k.r is compact notation the sum of the products of the components - sometimes because they were associating the r-vector only with spherical coordinates. The final page asks students to make a convincing argument for how the electric field is related to the magnetic field in terms of a cross-product with the wave vector – several students were initially trying to calculate the actual cross-product using determinants, without recognizing that the divergence and curl operations just replace the spatial derivatives with the corresponding components of k.
12A – Reflection & Transmission (Normal Incidence) (< 50 minutes)
Topics: Reflection and transmission, boundary conditions, complex exponentials.
Summary: Students begin by expressing in exponential notation the boundary condition on the parallel components of an EM plane wave for normal incidence at the interface between two media. They can then find the phase shift and amplitude for the reflected wave by considering representations of the electric field in the complex plane, first for when the amplitude of the transmitted wave is smaller than for the incident, and then when the opposite is true. Students should conclude that the frequencies of all three equations must match for the boundary condition to hold at all times. A second boundary equation is found by considering the electric and magnetic fields of the reflected wave. The remaining tasks connect the amplitude and phase shift of the reflected wave with the refractive indices of the two materials.
Comments: Warning (!): Portions of this tutorial have not been validated or field-tested, but we expect students to be able to finish the tasks in less than 50 minutes. A somewhat different version was used in our class, and the tasks related to representations in the complex plane are new. We anticipate that this way of representing the electric field will be more intuitive for seeing how the electric fields must match up in order for the boundary condition to be satisfied at all times. A number of students will have issues with the algebra when solving two equations for two unknowns on the final page. Checking their answers for the case when the refractive indices are equal may help them to see whether they have it right.
12B – Reflection & Transmission (Oblique Incidence) (~30 minutes)
Topics: Reflection and transmission, boundary conditions, complex exponentials.
Summary: Students begin by expressing in exponential notation the boundary condition on the parallel components of the electric field for an EM plane wave at oblique incidence to the interface between vacuum and a material. After finding the phase shift for the reflected wave, students should conclude that the components of k for each of the waves that are parallel to the boundary must match if the equation is true all along the boundary. The remaining tasks connect the angles of reflection and transmission to index of refraction for the material.
Comments: Warning (!): Portions of this tutorial have not been validated or field-tested, but we expect students to be able to finish these tasks in around 30 minutes. A somewhat different version was used in our class, and the tasks related to representations in the complex plane are new. The tasks in this tutorial have been constructed with the assumption that students have completed the tutorial on R&T for normal incidence (#12A); if not, the more abbreviated tasks herein will be more challenging, since they are not scaffolded in the same way as in the prior tutorial. The vectors in the diagrams all have the correct proportions, so it is important that students can justify their answers on the final page in terms of the reduced wave speed, and are not simply judging from the diagram.
13 – Gauge Invariance (< 50 minutes)
Topics: Time-dependent potentials and fields, gauge transformations
Summary: Students are first reminded of why EM fields can be written in terms of a scalar and vector potential. They then show that a gauge transformation in the vector potential results in an identical magnetic field. Students derive an integral relationship between E & A, and then find the necessary conditions for transforming V. A challenge question asks students to derive Poisson’s equation, which would be used to solve for the scalar function λ that transforms the potentials to the Coulomb gauge.
Comments: The biggest complaint from students has been about not entirely understanding why we would want to transform the potentials in the first place. This is hinted at in the final challenge question, where an equation is found for the function that transforms to the Coulomb gauge, but is not explicitly addressed here. The first task is a review intended to orient students to the remaining tasks, reminding them of why we can write the fields in terms of potentials. Many students have forgotten that the various statements that can be made about divergenceless (or irrotational) fields are all equivalent. [See Sect. 1.6.2 in Griffiths] Some students were unsure about the cross product being a linear operator (whether the curl of the sum of two vectors is equal to the sum of the curls). There has been a modest amount of confusion in simply keeping track of primed and unprimed quantities, with students sometimes mixing them up in their heads.
14 – Time-Retarded Potentials (~30 minutes)
Topics: Retarded time, time-retarded potentials and fields.
Summary: Students explore the concept of retarded time for the case of an infinitely long wire with a current that abruptly starts at t = 0. They first consider the points in space where an observer would be aware of there being a non-zero current a short time after it starts. Students find that the retarded time has different values at different points in space (relative to an observer at the origin), and decide on the limits of integration for finding the retarded vector potential at the origin. Challenge questions at the end have students calculate the electric field at the origin, and check their answer in the limit of long times.
Comments: Although it is fairly intuitive to students that it takes a finite amount of time for effects to propagate from a source to an observer, the definition of retarded time (and how it is used in a calculation) is not. In particular, that the retarded time is a function of two coordinate variables, and has different values at different points in space relative to a fixed observer. There is a “time ruler” on a separate handout that students can use for the questions on the first and second page – they may need a gentle reminder that it’s easiest to work with whole numbers for the distance from the origin (some were tempted to estimate the distance for points on the wire that were even with the tick marks on the x and y-axes). There were some students confused about what the primed and unprimed variables are each referring to, which typically shows up in problems involving the separation vector r - r'. The tasks in the challenge questions at the end are similar to Example 10.2 in Griffiths, but a simpler method (involving the fundamental theorem of calculus) is used for calculating the electric field from the retarded vector potential.
15 – Special Relativity
These are all relatively short activities, meant to address just some of the basics from special relativity, such as length contraction, 4-momentum, and velocity addition.
15A – Length Contraction (< 15 minutes)
Topics: Special relativity, Lorentz transformations, length contraction, simultaneity.
Summary: Students first establish the relationships between the times and locations that go into the length measurement of a moving body. They then derive a formula for length contraction using the Lorentz transformations, and consider whether the two position measurements occur at the same time in both frames.
Comments: Although some of the questions may seem trivial to instructors, we found that a number of students were confused on even the “simple” tasks, which shows that students may use the Lorentz transformations without understanding exactly what the different primed and unprimed variables correspond to. Our students were told beforehand that length measurements involve a simultaneous determination of the positions of the two ends; still, some were very tentative about simply saying that the two times are equal, or even that the length is simply the difference between the two position measurements.
15B – Inelastic Collision (~10 minutes)
Topics: Special relativity, 4-momentum, relativistic collisions.
Summary: Students use conservation of relativistic 4-momentum to find the final mass of an object resulting from the merging of two colliding particles.
Comments: This activity was straightforward for most students, as long as they were clear on the following: definition of relativistic 4-momentum; the total momentum of a system is the linear sum of the momenta of the particles; and that this quantity is conserved before and after the collision. Some students may momentarily forget the velocity dependence of γ when first working out the total momentum; the spatial velocities of the two particles cancel, but the γ-factor that appears in the total momentum is not also zero.
15C – Relativistic Velocity Transformation(~10 minutes)
Topics: Special relativity, Lorentz transformations, relativistic addition of velocities.
Summary: Students derive the velocity addition formula using the Lorentz transformations and the definition for the velocity in two different inertial frames.
Comments: The biggest difficulty for students may be the algebra involved. A common problem is for students to be confused about the velocity of the frame v, and the velocity of the particle u in that frame of reference. We have also noticed some conceptual difficulty for students regarding an event taking place at a single point in spacetime, and the different coordinate representations of that point in different inertial frames.
 E&M 2: Learning Goals
E&M 2: Learning Goals
E&M II Learning Goals
These learning goals for upper-division electrodynamics were created by a group of physics faculty from a number of research areas, including physics education research. Rather than addressing specific content to be covered in a course (as with a syllabus), this list of course-scale learning goals represents what we think students should be able to do at this stage of their development as physicists. The list of topic-specific learning goals reflects the knowledge and skills that were emphasiszed in the recent transformed E&M II courses at CU Boulder, organized according to their order of presentation in Griffiths.
- Build on earlier material: Students should deepen their understanding of introductory electromagnetism, junior-level E&M, and necessary math skills (in particular, vector calculus and differential equations).
- Maxwell’s equations: Students should see the various topics in the course as part of a coherent theory of electromagnetism; i.e., as a consequence of Maxwell’s equations.
- Math/physics connection: Students should be able to translate a description of a junior-level E&M problem into the mathematical equation(s) necessary to solve it; explain the physical meaning of the final solution, including how this is reflected in its mathematical formulation; and be able to achieve physical insight through the mathematics of a problem.
- Visualization: Students should be able to sketch the physical parameters of a problem (e.g., electric or magnetic fields, and charge distributions). They should be able to use a computer program to graph physical parameters, create animations of time-dependent solutions, and compare analytic solutions with computations. Students should recognize when each of the two methods (by hand or computer) is most appropriate.
- Organized knowledge: Students should be able to articulate the important ideas from each chapter, section, and/or lecture, thus indicating how they have organized their content knowledge. They should be able to filter this knowledge to access the information they’ll need to solve a particular physics problem, and make connections between different concepts.
- Communication: Students should be able to justify and explain their thinking and/or approach to a problem or analysis of a physical situation, in either written or oral form. Students should be able to understand and summarize a significant portion of an appropriately difficult scientific paper (e.g. an AJP article) on a topic from electromagnetism; and have the necessary reference skills to search for and retrieve a journal article.
- Problem-solving skills: Students should be able to draw on an organized set of content knowledge (LG#5), and apply problem-solving techniques (LG#11 below) with that knowledge in order to carry out lengthy analyses of physical situations. They should be able to connect all the pieces of a problem to reach a final solution. They should recognize the value for learning the material of taking wrong turns, be able to recover from their mistakes, and persist in working towards a solution even though they don’t necessarily see the path to that solution when they first begin the problem. Students should be able to articulate what it is that needs to be solved for in a given problem, and know when they have found it.
- Expecting and checking solutions: When appropriate for a given problem, students should be able to articulate their expectations for the solution, such as the magnitude or direction of a vector field, the dependence of the solution on coordinate variables, or its behavior at large distances. For all problems, students should be able to justify the reasonableness of a solution (e.g., by checking its symmetry, looking at limiting or special cases, relating to cases with known solutions, dimensional analysis, and/or checking the scale/order of magnitude of the answer).
- Derivations/proofs: Students should recognize the utility and role of formal derivations and proofs in the learning, understanding, and application of physics. They should be able to identify the necessary elements of a formal derivation or proof; and be able to reproduce important ones, including an articulation of their logical progression. They should have some facility in recognizing the range/limitations of a result based on the assumptions made in its derivation.
- Intellectual maturity: Students should accept responsibility for their own learning. They should be aware of what they do and don’t understand about physical phenomena and classes of problems, be able to articulate where they are experiencing difficulty, and take action to move beyond that difficulty (e.g., by asking thoughtful, specific questions).
- Problem-solving techniques: Students should be able to choose and apply the problem-solving technique that is appropriate for a particular situation (e.g., whether to use the integral or differential forms of Maxwell’s equations). They should be able to apply these methods to novel contexts (i.e., solving problems that do not map directly to examples in a textbook), indicating how they understand the essential features of the technique, rather than just the rote mechanics of its application.
...11a. Approximations: Students should be able to effectively use approximation techniques, and recognize when they are appropriate (e.g., at points far away or very close to the source). They should be able to decide how many terms of a series expansion must be retained to find a solution of a given order, and be able to complete a Taylor Series to at least two terms.
...11b. Symmetries: Students should be able to recognize symmetries, and be able to take advantage of them when choosing the appropriate method of solution (e.g., correctly applying the Maxwell-Ampere law to calculate the magnetic field of an infinitely long wire).
…11c. Integration: Students should be able to write down the line, surface or volume integral required for solving a specific problem, and correctly follow through with the integration.
...11d. Superposition: Students should recognize that – in a linear system – a general solution can be formed by the superposition of multiple components, and a specific solution found by applying appropriate boundary conditions.
Griffiths Ch 7: (Maxwell’s Equations, EMF, inductance, boundary conditions)
Students should be able to...
- …apply Stokes’ Law and the Divergence theorem, and be able to use them to convert equations from differential to integral form (and vice-versa), as well as interpret the physical meaning of the resulting terms (e.g., What's a flux? What's a divergence? What does the curl tell you?)
- …write down, and explain in words and pictures, the full set of Maxwell's Equations. This includes recognizing which are relevant for solving a given problem, and correctly using them to generate a solution. In particular, students should be able to use the integral form of Faraday’s Law to determine induced electric fields; and the Maxwell-Ampere law to find induced magnetic fields.
- …determine the total resistance or conductivity of a material for sufficiently symmetric geometries, calculate the total current flowing, and apply Ohm’s Law (J = σE) to relate the current density to the electric field.
- …state the continuity equation in differential and integral forms, explain how it is an expression of charge conservation, and understand its implications for quantities such as J and E in steady-state situations.
- …know how electromotive force is defined, and be able to compute EMF (either motional or Faraday-induced) for a variety of situations (typically with known or easily computed fields).
- …relate mutual and self-inductance to magnetic flux and the resulting induced EMF and currents, and find the mutual and self-inductance for a situation with sufficient symmetry.
- …set up and then solve the differential equations describing time-dependent circuit quantities (such as current, charge, voltage differences) for simple networks of resistors, capacitors, and inductors; and with AC or DC drivers.
- …work with complex exponentials in circuit analysis (phasor diagrams), and translate between complex (imaginary) solutions and physically real quantities.
- …calculate the total energy contained in electromagnetic fields from the energy densities, as well as compute the power and energy flow in AC circuits (by considering the energy stored in the fields, and dissipated in resistors).
- …translate between E- and B-fields and the auxiliary fields D & H, in terms of the polarization and magnetization of a material, and be able to set up appropriate boundary conditions to determine E, B, D & H at the interface of two different media.
Griffiths Ch 8: (Conservation laws for charge, momentum & energy)
Students should be able to...
- …physically interpret the continuity equation (LG 7.4), and be able to use the divergence theorem to express it in both integral and differential forms.
- …recall how Poynting's theorem is derived (what assumptions go into it, and the basic mathematical manipulations), and be able to physically interpret and use S, along with the energy density, to solve problems involving the transfer of energy through electric and magnetic fields.
- …qualitatively use the expression for momentum volume density, and explain its connection to conservation of momentum in EM systems (and similarly for angular momentum volume density).
Griffiths Ch 9 (9.1-9.3): (Electromagnetic waves, reflection and transmission, dispersion, EM waves in conductors)
Students should be able to:
- …construct general solutions to the wave equation, in 1-D to 3-D (including superposition solutions which might not look like the canonical "traveling wave"). For traveling waves, students should be familiar with the usual elements such as wavelength, wave vector, frequency and angular frequency, period, phase, polarization, and velocity.
- …derive the traveling wave equation (and thus its solutions) in free space and in matter, starting from Maxwell's Equations. This involves using the connections between E and B (and wave speed, wavevector, and polarization directions) as they arise from Maxwell's equations.
- …interpret and work with plane wave solutions in complex notation, and move back and forth between this notation and the real (physical) wave formulas, as well as apply concepts from previous chapters (S, energy, momentum and angular momentum densities) in the context of EM plane waves.
- …find the boundary conditions for EM waves at the interface of different media, starting from Maxwell's Equations, and apply them to solve for and interpret the reflected and transmitted waves, and their intensities (including understanding and working with the Brewster angle and Snell's Law).
- …state the assumptions that go into simple models for the complex index of refraction, and the associated equations for the dispersion and absorption of electromagnetic waves in dielectric and conducting media.
Griffiths Ch 10: (Potentials, gauge invariance, retarded time)
Students should be able to...
- …compute time-dependent fields, given the scalar and vector potentials.
- …qualitatively explain the concept and basic consequences of gauge invariance.
- …use the definitions of the Coulomb and Lorentz gauges, and be able to state/show how they lead to solvable wave equations.
- …state the definition of retarded time, and compute and interpret potential functions using the retarded time formalism in cases of very simple geometry.
Griffiths Ch 11: (Radiation) Students should be able to...
- …identify terms in mathematical expressions that correspond to radiation fields.
- …explain and justify both the math and physics of the “three approximations” made when calculating electric or magnetic dipole radiation.
- …use and explain the mathematical forms of E and B for electric or magnetic dipole radiation fields, including computation or representation of energy flow, intensity and power (with angular and radial dependence).
- …derive and use expressions for the “radiation resistance”.
- …qualitatively describe and use the basic Larmor formula for radiation from an accelerating point charge.
Griffiths Ch 12: (Relativity) Students should be able to...
- …clearly describe the two principles of relativity, and their basic consequences (e.g., the relativity of simultaneity, Lorentz contraction and time dilation).
- …use Lorentz transformations and four-vector notation to express observables in different inertial frames.
- …describe what makes a quantity invariant in the context of relativity, distinguish it from a conserved quantity, and use both concepts to compute relativistic kinematics problems.
- …interpret and sketch space-time diagrams, and connect them to mathematical formulas.
- …use appropriate transformations to convert electromagnetic fields and potentials between inertial frames.
 E&M 2: Research Associated with the Course
E&M 2: Research Associated with the Course
Publications
(Includes publications for both E&M 1 and 2)
- S. Chasteen, Teasing out the effect of tutorials via multiple regression, presented at the Physics Education Research Conference 2011, Omaha, Nebraska, 2011.
- S. Chasteen, R. Pepper, M. Caballero, S. Pollock, and K. Perkins, Colorado Upper-Division Electrostatics diagnostic: A conceptual assessment for the junior level, Phys. Rev. ST Phys. Educ. Res. 8 (2), 020108 (2012).
- S. Chasteen, R. Pepper, S. Pollock, and K. Perkins, But Does It Last? Sustaining a Research-Based Curriculum in Upper-Division Electricity & Magnetism, presented at the Physics Education Research Conference 2011, Omaha, Nebraska, 2011.
- S. Chasteen, K. Perkins, P. Beale, S. Pollock, and C. Wieman, A Thoughtful Approach to Instruction: Course transformation for the rest of us, J. Coll. Sci. Teaching 40 (4), 24 (2011).
- S. Chasteen and S. Pollock, Transforming Upper-Division Electricity and Magnetism, presented at the Physics Education Research Conference 2008, Edmonton, Canada, 2008.
- S. Chasteen and S. Pollock, A Research-Based Approach to Assessing Student Learning Issues in Upper-Division Electricity & Magnetism, presented at the Physics Education Research Conference 2009, Ann Arbor, Michigan, 2009.
- S. Chasteen and S. Pollock, Tapping into Juniors’ Understanding of E&M: The Colorado Upper-Division Electrostatics (CUE) Diagnostic, presented at the Physics Education Research Conference 2009, Ann Arbor, Michigan, 2009.
- S. V. Chasteen, S. J. Pollock, R. E. Pepper, and K. K. Perkins, Thinking like a physicist: A multi-semester case study of junior-level electricity and magnetism, 80 (10) 923-930 (2012).
- S. Chasteen, S. Pollock, R. Pepper, and K. Perkins, Transforming the junior level: Outcomes from instruction and research in E&M, Phys. Rev. ST Phys. Educ. Res. 8 (2), 020107 (2012).
- J. Huffman, M. Vignal, and B. Wilcox, Investigating Upper-Division Students' Interpretations of the Divergence Theorem, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
- R. Pepper, S. Chasteen, S. Pollock, and K. Perkins, Our best juniors still struggle with Gauss’s Law: Characterizing their difficulties, presented at the Physics Education Research Conference 2010, Portland, Oregon, 2010.
- R. Pepper, S. Chasteen, S. Pollock, and K. Perkins, Observations on student difficulties with mathematics in upper-division electricity and magnetism, Phys. Rev. ST Phys. Educ. Res. 8 (1), 010111 (2012).
- K. Perkins and C. Turpen, Student Perspectives on Using Clickers in Upper-division Physics Courses, presented at the Physics Education Research Conference 2009, Ann Arbor, Michigan, 2009.
- S. Pollock and S. Chasteen, Longer term impacts of transformed courses on student conceptual understanding of E&M, presented at the Physics Education Research Conference 2009, Ann Arbor, Michigan, 2009.
- S. Pollock, S. Chasteen, M. Dubson, and K. Perkins, The use of concept tests and peer instruction in upper-division physics, presented at the Physics Education Research Conference 2010, Portland, Oregon, 2010.
- S. Pollock, R. Pepper, S. Chasteen, and K. Perkins, Multiple roles of assessment in upper-division physics course reforms, presented at the Physics Education Research Conference 2011, Omaha, Nebraska, 2011.
- S. Pollock and B. Wilcox, Upper-Division Students' Use of Separation of Variables, presented at the Physics Education Research Conference 2015, College Park, MD, 2015.
- Q. Ryan, C. Baily, and S. Pollock, Multiple-Response Assessment for Upper-division Electrodynamics, presented at the Physics Education Research Conference 2016, Sacramento, CA, 2016.
- C. Wallace and S. Chasteen, Upper-division students' difficulties with Ampère's law, Phys. Rev. ST Phys. Educ. Res. 6 (2), 020115 (2010).
- B. Wilcox, M. Caballero, R. Pepper, and S. Pollock, Upper-division student understanding of Coulomb's law: Difficulties with continuous charge distributions, presented at the Physics Education Research Conference 2012, Philadelphia, PA, 2012.
- B. Wilcox, M. Caballero, D. Rehn, and S. Pollock, Analytic framework for students’ use of mathematics in upper-division physics, Phys. Rev. ST Phys. Educ. Res. 9 (2), 020119 (2013).
- B. Wilcox and S. Pollock, Multiple-choice Assessment for Upper-division Electricity and Magnetism, presented at the Physics Education Research Conference 2013, Portland, OR, 2013.
- B. Wilcox and S. Pollock, Upper-division student difficulties with the Dirac delta function, Phys. Rev. ST Phys. Educ. Res. 11 (1), 010108 (2015).
- B. Wilcox and S. Pollock, Validation and analysis of the coupled multiple response Colorado upper-division electrostatics diagnostic, Phys. Rev. ST Phys. Educ. Res. 11 (2), 020130 (2015).
- J. Zwolak and C. Manogue, Revealing Differences Between Curricula Using the Colorado Upper-Division Electrostatics Diagnostic, presented at the Physics Education Research Conference 2014, Minneapolis, MN, 2014.










