Research-based worksheets for introductory physics that help students
-
build on their own good ideas as “seeds of science”,
-
engage in sense-making about physics, and
-
develop and apply models of key physics concepts.
Open-access and editable so you can customize for your classroom and students.
Get the ACORN Physics Tutorials
Design and structure of ACORN Physics Tutorials
ACORN Physics Tutorials are worksheets that students work on collaboratively in groups of 3-4 with support from instructors and/or near-peer facilitators. Each takes 50-90 minutes for students to complete. Three types of questions guide students to build their own models for common physics phenomena:
To learn more, see instructor resources.
Tutorials
Classroom videos featuring ACORN Physics Tutorials
These short video clips and training lessons can give instructors a sense of how students learn with ACORN tutorials. Watch the short video clips to understand what student might do and discuss, and use the sample discussion prompts to prepare yourself to teach with these Tutorials.
 What enables students to answer their own questions?
What enables students to answer their own questions?
 How do students build new ideas?
How do students build new ideas?
 Should I help students solve problems efficiently?
Should I help students solve problems efficiently?
Introduction
 Here is a series of conceptual questions that draw out a variety of conceptual resources, which are potentially generative student ideas or “seeds of science” that can grow toward sophisticated understandings with support and cultivation. These questions could be used as discussion questions in an introductory physics course, or as homework or quiz questions. We recommend using these when beginning a new topic, to learn about your students' ideas. Many of these questions are featured in ACORN Physics Tutorials, but some are not and could be used in conjunction with the Tutorials to further advance resources-oriented instruction. For each question, we include:
Here is a series of conceptual questions that draw out a variety of conceptual resources, which are potentially generative student ideas or “seeds of science” that can grow toward sophisticated understandings with support and cultivation. These questions could be used as discussion questions in an introductory physics course, or as homework or quiz questions. We recommend using these when beginning a new topic, to learn about your students' ideas. Many of these questions are featured in ACORN Physics Tutorials, but some are not and could be used in conjunction with the Tutorials to further advance resources-oriented instruction. For each question, we include:
- A downloadable (and editable) PowerPoint slide with the question.
- Information for instructors about the question design and our answer to the question.
- A few sample student responses and an overview of some of the conceptual resources we observe students using and how we perceive these resources to be connected to introductory physics learning goals.
Linear momentum questions
 Ball/clay predict question
Ball/clay predict question
The ball/clay predict question tells students to suppose they want to close a door quickly but cannot reach it. The question then asks whether they would choose to throw a rubber bouncy ball or an equally massive piece of clay at the door to accomplish this task.
Information for instructors:
The ball/clay predict question is a predict-style question, a type of question that asks students to apply principles and ideas to a new scenario. Our own answer to this question is that the ball will move more quickly if we choose to throw the rubber bouncy ball. With the door initially at rest, the initial momentum of the system is the momentum of the clay/ball. If we assume these initial momenta are the same (e.g., we throw them with the same speed in the same direction and they are equally massive), then the vector representing the momentum of the system points in the same direction and is the same length for both scenarios. The clay sticks to the door and continues to have a component of motion in its original direction, and the rubber ball bounces and moves in the opposite direction. By vector addition, the final momentum of the door (which moves in the ball’s original direction of motion) would be higher with the rubber ball.
Common ideas and sample student responses:
Students used a variety of conceptual resources in their responses to this question, ranging from applying rules and constraints they may have learned in physics class (using terms like “isolated system,” “momentum conservation,” and “elastic and inelastic collisions”), to sense-making about what an inelastic or elastic collision is (drawing on ideas of force and energy). For example, one student wrote:
“The momentum when it approaches the door is positive. Assuming this happens in a closed system, momentum is conserved. So, when the bouncy ball hits the door, it moves in a negative direction & has a negative momentum, causing the door to have a positive momentum in the opposite direction.”
This (correct) written student response illustrates attention to both the conservation and the directionality of momentum at different moments during and after the collision.
Another student wrote:
“The [motion of the door will be the] same. When they [rubber ball and clay] collide the door, the momentums of the door change in the same magnitude because they have the same mass.”
This student reasons that since the rubber ball and clay are equally massive, the door they hit will experience equal changes in the magnitudes of momentum. While this response is canonically incorrect, the student is both (i) considering a property of the objects (mass) that are relevant to momentum and (ii) recognizing that the properties of the object matter for what happens in a collision between them. Many students used similarly structured arguments, reasoning that because the objects that collided have a certain property (hard, soft, bouncy, heavy, light, fast, etc.), their momentum changes in a certain way.
Some students provided a mechanism that explained why they thought either the rubber ball or the clay would shut the door more quickly. For example:
“I would throw the piece of clay at the door because it wouldn’t bounce off as much. More momentum would be transferred from the clay.”
This student (and others like them) reasoned that because the clay stuck to the door, it transfers more of its momentum to the door. Other students answered that the bouncy ball has more oomph and so transfers more of its momentum to the door, or that bouncy objects can change their momentum more.
In short, the ball/clay predict question appears to elicit resources for conservation, directionality, and identifying the kind of collision at play, as well as mechanisms that students use to explain why one collision or the other might transfer more energy or momentum.
 Desk chair momentum predict question
Desk chair momentum predict question
The desk chair momentum predict question tells students that two people are facing one another in desk chairs with low-friction bearings and that one of the people tosses a large, heavy ball to the other. They are asked whether the student who tosses the ball will remain at rest, and whether the student who catches the ball will remain at rest.
Information for instructors:
This predict-style question is similar (but not identical) to questions found on the Energy and Momentum Conceptual Survey and the Force and Motion Conceptual Survey. Our answer to the desk chair momentum predict question is that the student who tosses the ball will begin moving opposite the direction they toss the ball, and the person who catches the ball will begin moving in the direction of motion of the ball as they catch it. We can make sense of the catcher’s movement in terms of momentum transfer: when the ball collides with the person, it gives some of its momentum to the person, and they begin to move. The ball and the person move more slowly than the ball did originally because of momentum conservation: when the ball gives some momentum to the person, it moves slower. The person is presumably more massive than the ball and receives only a part of the ball’s momentum so also moves slower than the ball did. For the thrower: the original (vector) momentum of the system was zero. When the ball moves one way, the thrower must move the other way to conserve momentum.
Common ideas and sample student responses:
The desk chair predict question elicited a variety of resources, often relating to momentum conservation and transfer. Some of these resources resembled rules or procedures: momentum is conserved, momentum can transfer, analysis of systems, or efforts to “balance” or “equalize” momentum (connected to, but not precisely, momentum conservation). Others resembled mechanisms for momentum transfer (e.g., forces). For example:
“No. They will both move farther apart. For the first, momentum one way leads to momentum the other way. Second, the momentum of [the] ball transfers to the person.”
This response uses a sort of “momentum balancing,” reminiscent of (and a resource for) momentum conservation, to determine that the thrower will move opposite the direction of motion of the tossed ball. They use momentum transfer (which implies conservation) to decide that the catcher will also move.
Another student responded:
“If you break the situation into two different systems: the thrower and the catcher, the thrower system is elastic and the catcher system is inelastic. This helps us because when looking at the thrower system, the thrower is initially at rest but then when throwing the ball we know that momentum needs to be conserved so the student will move backwards canceling out the motion of the ball. Then when the other student catches both the student and ball ‘stick’ together and move in the same direction.”
This response draws on a variety of resources, including identifying systems, to conclude that both the thrower and the catcher will move. They name two relevant systems for this scenario – (1) the thrower and the ball and (2) the catcher and the ball – and identify one collision as elastic and the other as inelastic. Though it’s not totally what this student means by “elastic” and “inelastic,” they are drawing on resources for identifying systems and types of collisions that connect with learning objectives in introductory physics in ways that instructors might build on.
Some students drew on Newton’s third law to make sense of the direction of motion of the thrower and the catcher. For example:
“No - neither remains at rest. Both catching and throwing the ball requires a force and these forces come in equal/opposite pairs, so applying a force to move the ball/slow it down will also apply a force to you in the chair that moves you.”
Here, the student argues that as the thrower applies a force to move the ball, the ball exerts an equal and opposite force on the person, such that the person will move (accelerate) in the direction opposite the ball’s motion. Likewise, when the catcher applies a force opposite the ball’s motion to slow it down upon catching it, the ball applies an equal and opposite force to the catcher, accelerating the catcher in the direction of the ball’s motion.
In summary, the desk chair momentum predict question appears to elicit resources for momentum conservation and transfer, as well as resources that connect forces and energy to momentum, all goals of introductory physics instruction in the context of linear momentum.
Circuits questions
 Rank the bulbs explain question
Rank the bulbs explain question
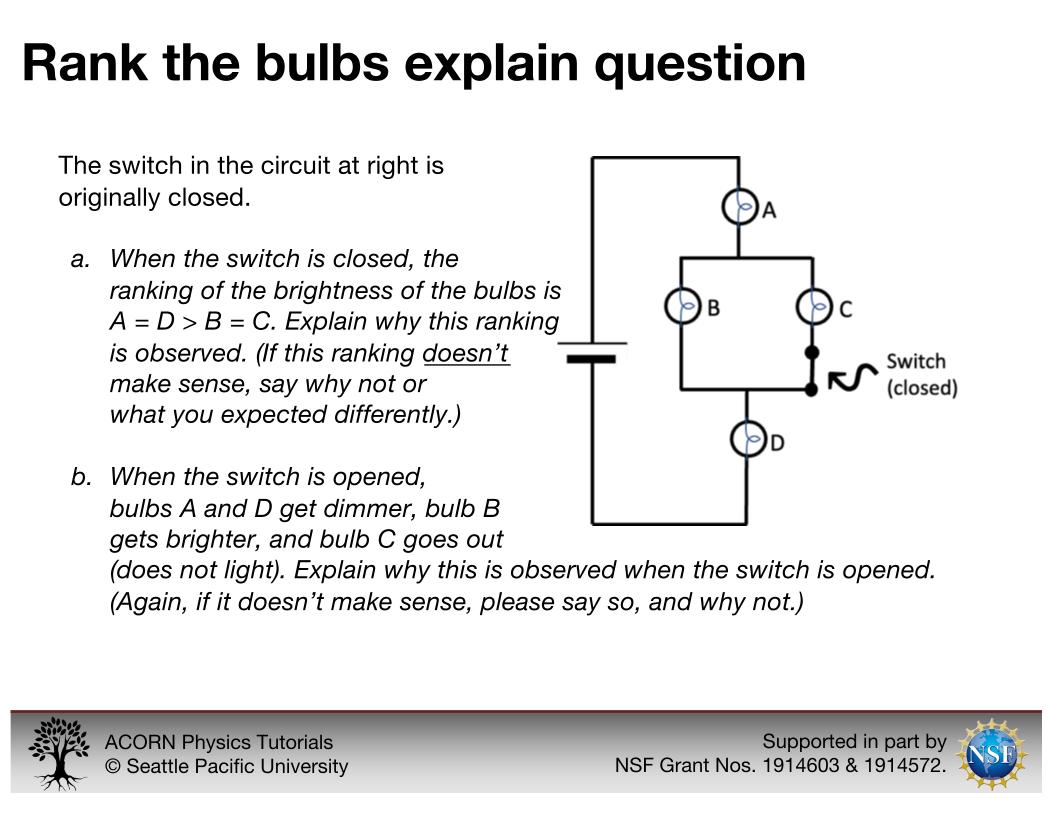
The rank the bulbs explain question shows students a circuit with four bulbs and a switch, and ranks the brightness of the bulbs when the switch is closed (part a) and then opened (part b). Students are asked to say why the rankings are observed.
Information for instructors:
This question is featured in our ACORN Physics circuits tutorial and in our research (Bauman et al. 2024), and in using it there and elsewhere, we sometimes find that it can help to break question (b) into several parts, highlighting the dimming of bulbs B and C, the brightening of bulb A, and bulb D going out altogether separately. This is an explain-style question that describes a phenomenon and asks students to sense-make about it, rather than to predict a particular outcome. It was adapted from McDermott and Shaffer 1992. Our own answer to this question relies on current tracing and Ohm’s Law: in the original (closed switch) circuit, all of the current from the battery goes through bulb A, then splits equally through bulbs B and C (which are identical), then recombines to go through bulb D. This makes B and C equally bright but dimmer than A and D, which are themselves equally bright (since the current is conserved as it splits and recombines). When the switch is opened, the branch with bulb C is no longer complete, and what was originally a two-bulb parallel circuit element becomes a single-bulb series element, such that the circuit is effectively a three-bulb series circuit. This increases the resistance, decreasing the current through the battery. Thus bulbs A and D, which originally received all of the current from the battery, dim. Bulb B, now in series with the battery, brightens, and bulb C does not light.
Common ideas and sample student responses:
Students used a variety of resources for understanding current, voltage, and resistance to answer this question. Most commonly, students focused on current as responsive to changes in the circuit (including different connections) and resistance as limiting current. For example:
“...when the switch opens, bulb B joins the series instead of just being in parallel to bulb C, so resistance increases. The battery is the same so V remains the same. Therefore current must decrease to compensate.”
This response acknowledges that the way the circuit elements are connected matters for the properties (in particular, the resistance) of the circuit, naming that the resistance increases if you take away a parallel branch. The student draws on the resource that current is responsive to changes in the circuit; when voltage remains the same but resistance increases, “current must decrease to compensate.”
Another student wrote:
“When the switch is opened, the current no longer has the option to split and flow through either B or C, it must all flow through B. Since B and C are no longer in parallel, the overall resistance of the circuit is greater than when the switch is closed. With greater resistance, there is less current according to Ohm’s Law. And since the luminosity of a light bulb is directly proportional to current, this means dimmer light bulbs as well.”
Here, the student uses current tracing (conservation of current) to analyze how changing the connections in the circuit will change how the current moves through. Like the previous response, this student acknowledges that removing a parallel branch increases the resistance of the circuit, which increases the current by Ohm’s Law.
As might be expected with complex circuits that contain many elements, students’ analyses in the rank the bulbs explain question include multiple parts that include a variety of resources. We are especially interested in the ways in which these responses articulate a nascent conceptual model of current as responsive to changes in the circuit (including changes in resistance and changes in how elements are connected to one another), a resource that appears to be consistently activated in this context.
 Order of elements explain question
Order of elements explain question
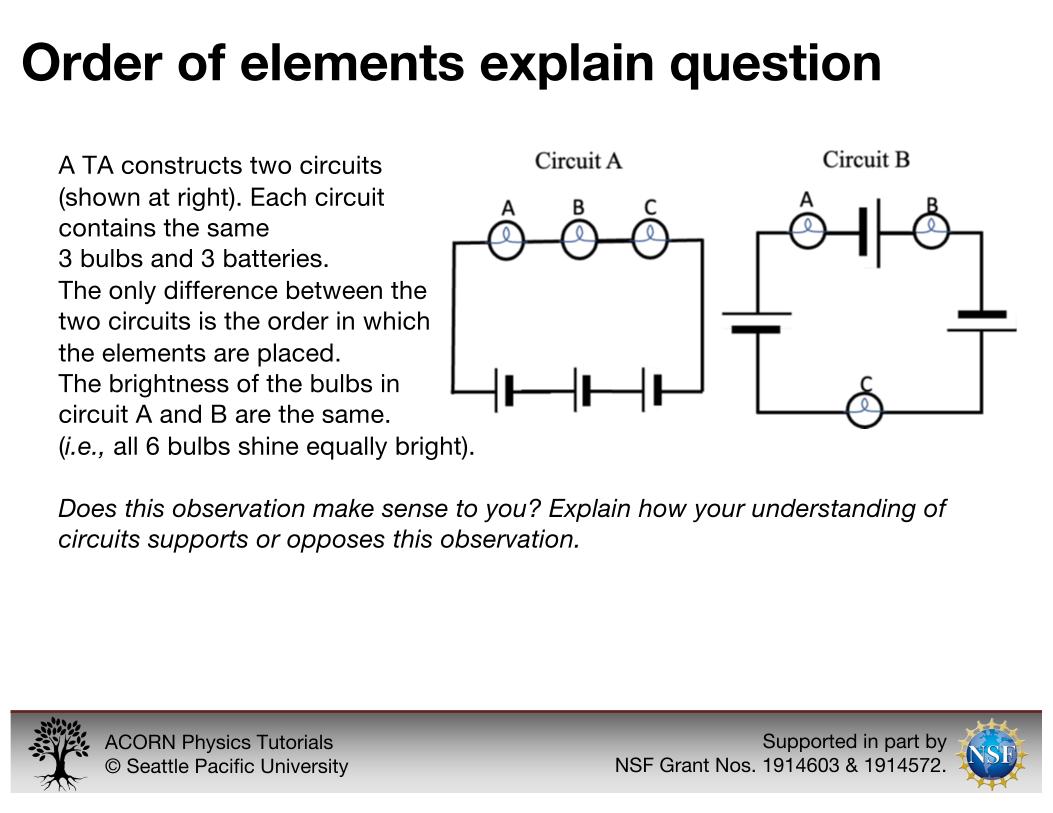
The order of elements explain question shows students two circuits, both of which have three batteries and three bulbs in series, with all of the batteries facing the same direction. However, in the second circuit, rather than having three bulbs then three batteries in a row, the elements are arranged bulb-battery-bulb-battery-bulb-battery. Students are told that all six of the bulbs in the two circuits are equally bright and are asked why this is the case.
Information for instructors:
The order of elements explain question is an explain-style question that asks students to make sense of the observation that the order of batteries and bulbs in a circuit does not impact the brightness of the bulbs.
Common ideas and sample student responses:
As with the rank the bulbs explain question, students drew on resources that highlighted that current is responsive, this time also foregrounding that voltage drives current, alongside attending to resistance as opposing current and the connections between elements as relevant. For example:
“[...] In circuit A, the batteries are all in a row which increases the total current but the resistors are also in a row which would decrease the total current. Circuit A has 3 times the voltage but also 3 times the resistance, which would result in the same current. Circuit B also has the same current because the voltage is one and the resistance is 1, but it happens three times in series.”
Though it isn’t clear to us how this student calculated the voltage and resistance (as 1 for Circuit B, and as “three times” for Circuit A), it is clear that they are framing voltage as driving current, resistance as limiting it, and current as responsive to both. It may be that they think of the current as going up and then down (changing as it moves through the circuit); whether or not this is the case, we can identify resources in this response that we could leverage to support conceptual understanding of voltage, current, and resistance.
Similar notions of voltage as driving current and resistance as limiting it are observed in this student response:
“[It] makes sense [that all the bulbs are the same brightness] because the current is the same everywhere in the wire and is being pushed forward by the same amount of voltage from the batteries and resisted by the same amount of resistance.”
This student justifies not only that the current should be the same in the two circuits, but also that the current should be the same throughout each circuit, using language of “pushed” (for voltage) and “resisted” (for resistance).
Some students focused on the two circuits having similar types of connections (rather than, say the same numbers and types of elements). For example:
“[...] Since electrons flow as a stream through the wire, the positioning of the components doesn’t matter in this case. The “stream” is being slowed down by the bulbs, and pushed by the batteries, doesn’t matter where. In tug of war for example, it doesn’t matter much where you position the people pulling, as long as they are somewhere on the rope.”
Here the student models electrons as a stream flowing through the wire, extending that model to then say that the positioning of the elements doesn’t matter. They advance this model by saying that the effect of the elements is to push, in the case of batteries, and slow things down, in the case of resistors, and it doesn’t matter where in the “stream” (or the rope, in their tug-of-war analogy) this happens; it just matter that it does.
Both the rank the bulbs explain question and the order of elements explain question provide contexts for eliciting a conceptual model for current as responsive to elements and their order, resistance as limiting current, and voltage as driving current. The order of elements question appears to foreground voltage-as-driver more than the rank the bulbs question, which appears to more frequently cue the resistance-as-limiting resource, at least for the samples of student responses we analyzed.
Mechanical waves questions
 Tension pulse flick question
Tension pulse flick question
The tension pulse flick question gives students two scenarios: one in which a TA creates a pulse by flicking a spring attached to a wall, and the second in which the same TA pulls the spring taut and flicks the spring in the same way, creating a second pulse that propagates down the spring more quickly. The question asks students why it would make sense for a pulse to move faster on a higher-tension spring.
Information for instructors:
The tension pulse flick question is an explain-style question that provides a description of an observation and asks students to say why it makes sense (or doesn’t) to them. The question is a revised version of a question on the Waves Diagnostic Test. Our answer to the tension pulse flick question is that as the spring becomes more taut, the (tension) forces between adjacent parts of the spring increase, such that when one part of the spring is displaced by the disturbance, it pulls the adjacent parts more, and the pulse is propagated down the spring more quickly.
Common ideas and sample student responses:
Student responses to the tension pulse flick question drew on resources that highlighted the ways in which the properties of the medium affect the motion of the pulse, that focused on the up-and-down motion of the spring as the way in which the pulse propagates (and how this motion is affected by changes to the properties of the spring), and that brought in ideas about forces and energy to explain changes in the speed of the pulse. For example:
“The higher the tension of the spring, the more sensitive it is to movement so the pulse can travel faster.”
This student explains that the speed of a pulse depends on the tension in the medium because increased tension means the medium can react more quickly to the pulse. The student goes beyond naming the relationship between tension and pulse speed, toward a nascent causal association.
Other students focused on the forces between parts of the spring, as we did in our answer to the tension pulse flick question. For example:
“When the tension is higher, the particles (or small part[s]) of the springs are pulling each other with more forces. If one particle goes upward, then the particle next to it will be dragged upward. With more forces (= higher tension), it gets dragged even faster (tightly bound). This speed of getting dragged is the speed of the wave, so the higher the tension [the] higher the speed. (c = T/, with same μ.)”
In focusing on a “point,” a “particle,” or a “part” of the spring, this response implies a discretized model of the medium. The student argues that increasing tension makes each particle accelerate more quickly, increasing the wave speed, drawing on reasoning about forces to make sense of pulse propagation.
Students sometimes used reasoning about energy to make sense of faster pulses on higher-tension springs. For example:
“Having a tighter string means less energy gets represented as vertical displacement so that more energy goes into the pulse’s forward movement, i.e., speed.”
In this example, as in many sample textbook solutions that encourage students to break up the energy of a system into its varied forms, the student reasons that in pulse propagation, some energy is in the form of vertical displacement and some in the form of forward movement. When the tension is increased, they reason, the pulse does not go as high, so more energy is able to be “put into” forward movement. Though incorrect, this response associates energy with the shape (“vertical displacement”) of the spring, and associates the speed of the pulse with the tension in the medium, reasoning that energy is associated with or carried by the pulse itself and that energy transfers and transformations play a role in the speed or motion of the pulse.
In general, our experience is that the tension pulse flick question elicits ideas that support student thinking about how propagation happens and why the medium and its properties matter, often drawing on mechanics concepts like force and energy in sense-making.
 Mass density pulse flick question
Mass density pulse flick question
The mass density pulse flick question is very similar to the tension pulse flick question, except the property that is changed between the first and second scenario is the mass density–not the tension–of the spring. In particular, the TA replaces the first spring with a second one that has a higher mass density, and observes that the second pulse moves more slowly down the spring. Students are asked why it would make sense for a pulse to move more slowly down a spring with higher mass density.
Information for instructors:
The mass density pulse flick question, like the tension pulse flick question, is an explain-style question. Our answer to this question is again based on a model in which a pulse propagates by pulling on adjacent parts of the spring. If the tension (and thus the forces between parts) of two springs is the same, but the mass of the parts of one spring is more than the other, the accelerations of the pieces of the more massive spring will be smaller, and the pulse will propagate more slowly.
Common ideas and sample student responses:
As with the tension pulse flick question, student responses to the mass density pulse flick question drew on resources that highlighted the ways in which the properties of the medium affect the motion of the pulse, that focused on the up-and-down motion of the spring as the way in which the pulse propagates (and how this motion is affected by changes to the properties of the spring), and that brought in ideas about forces and energy to explain changes in the speed of the pulse. For example:
“Springs have inertia and heavier springs will have more inertia because inertia is proportional to mass. Since inertia is the tendency to resist change in motion, a heavier spring will oppose the motion of a pulse more.”
This example draws on ideas from mechanics–particularly inertia or a “tendency to resist change in motion”–to make sense of why the speed of the pulse would decrease as the mass density increases.
As in the tension pulse flick question, some students analyzed the spring as a series of discrete chunks, and sense-made about how an increase in mass density would affect the interactions between chunks. For example:
“It would make sense for the pulse to move more slowly on a heavier spring because you could represent each point of mass on the string with a free body diagram and the Fnet on each point of mass is equal to mass times acceleration. (Fnet = ma) Therefore, if the Fnet on each spring is the same as scenario 1, when the mass increases in scenario 2, the acceleration must decrease to compensate. This means that each point on the spring will accelerate more slowly when moving away from the ‘center line’ of the spring, effectively resulting in the pulse moving more slowly.”
This student response closely resembles the answer we offered, adding a reference to the displacement from the spring’s equilibrium.
Also similar to the tension pulse flick question, a number of students performed an energy analysis, splitting the energy among types of movements and reasoning about how changing the mass would affect this split. For example:
“In a heavier spring, there is more mass in a given unit of length. It would take more energy to displace this mass than in a lighter spring. Since more energy is spent on actually displacing the spring in a wave there will be less energy to drive the pulse’s velocity, given that the same amount of energy was applied each time.”
Here, the student reasons that it would take more energy to move a higher-mass chunk (“a given unit of length”). This would leave less energy to “drive the pulse’s” forward movement, and therefore the pulse would propagate more slowly. Though not necessarily canonically correct, this response productively associates energy with the dynamics of pulse propagation.
In our experience, both the tension and mass density pulse flick questions offer an opportunity for students to go beyond understanding that propagation speed is the square root of tension divided by mass density, toward reasoning about how the properties of the medium affect the speed of the pulse. In many cases this reasoning includes modeling the medium as a discrete series of chunks that interact with one another, modeling the pulse as a disturbance that moves these chunks up and down, and drawing on the concepts of forces and energy to explain the dynamics of pulse propagation.
 Fixed end reflection question
Fixed end reflection question
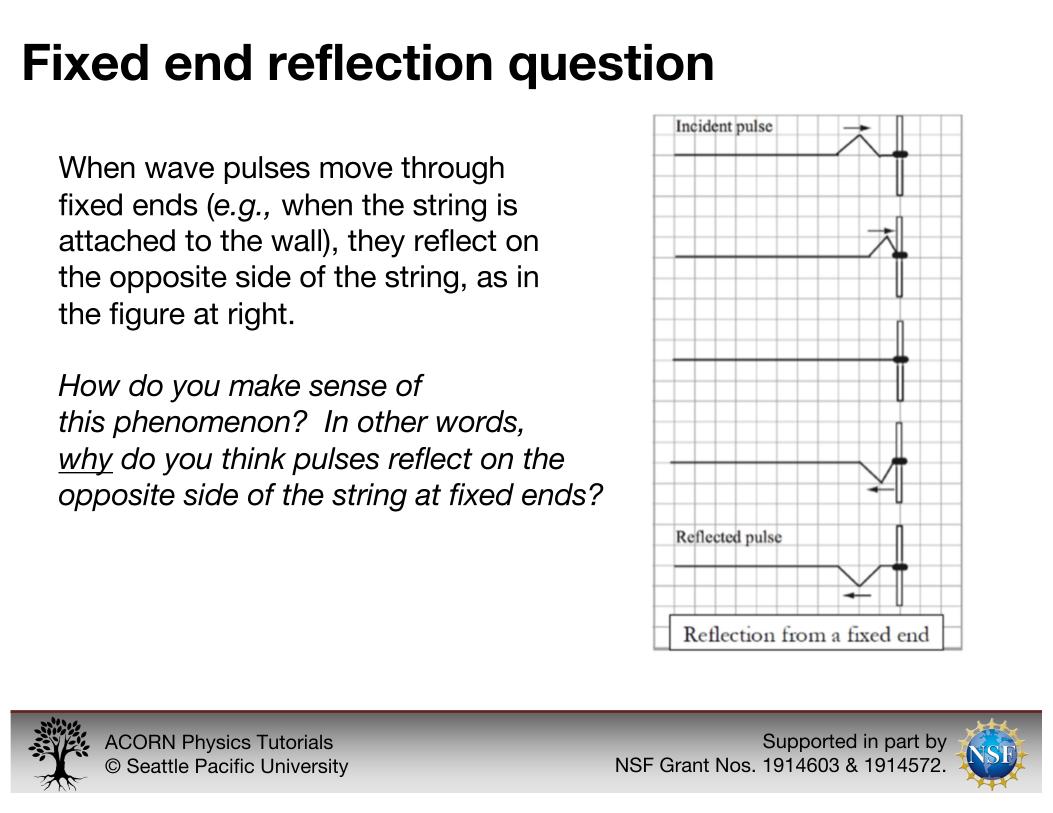
The fixed end reflection question tells students that pulses reflect on the opposite side of the spring at fixed ends, and then asks them why they think that happens.
Information for instructors:
This is an explain-style question. In answering the fixed end reflection question ourselves, at a level that is appropriate for introductory physics students, we analyze the forces on the spring at the fixed end. As the pulse reaches the fixed end, the spring pulls up on the wall, and Newton’s third law tells us that the wall pulls back on the spring, exerting a force downward on the segment of spring that is adjacent to the wall. The downward force from the wall is greater than the upward force from the segment of spring on the other side, the segment closest to the wall accelerates downward and overshoots equilibrium to the other side.
Common ideas and sample student responses:
As we anticipated, students often used the concepts of forces and energy to explain the behavior of pulses at fixed ends, constructing responses with varying degrees of mechanism. For example, one student wrote:
“Every action has an equal and opposite reaction. So as the wave propagates towards the wall, and hits the wall, there is a force upwards on the wall. This means the wall exerts a force downwards on the string. Because F = m(dv/dt) and the wall does not accelerate, the string accelerates downwards, effectively inverting the wave. Also, maybe something to do with energy, ID[on’t]K[now].”
This response applies Newton’s second and third laws to the part of the string near the boundary (the wall), arguing that the pulse is inverted because the string pulls up on the boundary, and the boundary pulls down with an equal and opposite force, which causes the string to accelerate and move past the equilibrium point.
Other students applied energy concepts to reason about reflection on the opposite side of a spring at a fixed end. For example:
“… I believe that the reason it reflects to the other side is due to conservation of energy. Because the wave constantly wants to displace upwards, however [it is] unable to b/c of [the] fixed end. The only way it can go to maintain its energy is to deflect downward. Furthermore, energy has no direction, nor does it care about direction, therefore reflecting downwards does not change the energy state.”
Here, the student argues that conservation of energy requires that a pulse continue (it can’t just disappear), and since it can’t keep going up at the fixed end, it has to “deflect downward.” They add that because energy doesn’t have a directionality (only a magnitude), the top and bottom of the spring are effectively the same.
Some responses to the fixed end reflection question used procedures–such as modeling the reflected pulse as the superposition of the “incoming” pulse and an inverted “ghost” pulse–but this was less common than responses that drew on concepts of forces, motion, and energy to explain why the reflected pulse was on the opposite side of the spring. This suggests to us that the fixed end reflection question may support students in bridging ideas from mechanics to sensemake about fundamental pulse reflection phenomena.
 Superposition mechanism question
Superposition mechanism question
Like the tension pulse flick question, the mass density pulse flick question, and the fixed end reflection question, the superposition mechanism question is an explain-style question that describes a fundamental wave mechanics scenario and asks students why they think it happens that way. In particular, the superposition mechanism question tells students that when two pulses on the same side of a spring meet, they add–an example of superposition. They are then asked why pulses add when they are on the same side of the spring, or why superposition works the way it does.
Information for instructors:
Our hope was that students would go beyond restating the principle of superposition (mathematically or conceptually) and instead draw on mechanics principles to sensemake about the phenomenon. Our answer to the superposition mechanism question is that the leading edge of each pulse pulls upward on the segment of spring between them just before they meet. The force by each leading edge on this “middle segment” is determined by the tension in the spring and the shape of each pulse (sharper pulse means higher force). This means the “middle segment” accelerates in a way that is determined by the sum of the forces delivered by each leading edge. This kind of logic can be extended to the entire time period that the pulses overlap, leading to the same conclusions that the mathematical principle of superposition does.
Common ideas and sample student responses:
As we had hoped, students did draw on mechanics concepts–particularly forces, energy, speed, and acceleration–to explain why pulses add when they are on the same side of the spring.
“If the strings are both accelerating up, they will both accelerate up with twice the force.”
This response makes sense of superposition using the acceleration of parts of the spring. When two pulses that are both accelerating the spring up superpose, the string then “accelerate[s] up with twice the force,” making the string move even higher.
Another student responded using imagery of free body diagrams, writing:
“Imagine that the two pulses are forces acting upon an object in the same direction. [Drawing of box with two arrows whose tails are on the right side of the box and heads are pointing horizontally outward from there.] The total force on the object would be the sum of these two forces (constructive interference).”
Here, the student analogizes constructive interference to a sum of forces, where the spring is the object and the pulses are forces. When the forces are in the same direction, the spring experiences a net force that is the sum of those two forces, displacing it further.
Yet other students used energy to sensemake about superposition. For example, one student wrote:
“This principle is in line with the conservation of energy, if they weren’t added together, energy in the wave would be lost.”
While this response isn’t as clearly mechanistic (to us) as responses that draw on acceleration and forces, it does associate energy with the amplitude of the pulse, and uses conservation rules to sensemake about why the pulses can’t just disappear.
Some students also drew on resources for reasoning about what a pulse is, arguing that pulses superpose because they can occupy the same space at the same time (in contrast to, say, discrete objects).
“Superposition works because waves can occupy the same space at a given time therefore the net wave is the sum of the waves. Since the waves are on the same side, their displacements are (in this case) ‘positive’ and we add the pulses.”
These responses are less obviously about what makes pulses add when they are on the same side of the spring and are more clearly about what it is about pulses that makes it possible for them to add in the first place. This ontological characterization of pulses as not-objects challenges some of the findings from misconceptions-oriented studies of student understandings of waves, suggesting that the extent to which students think of pulses as objects depends on the context (Robertson et al. 2019).
In short, the superposition mechanism question, like the other waves questions we’ve offered here, may be especially appropriate for supporting connections between mechanics ideas and wave dynamics, and (in this case) for eliciting ideas about the nature of pulses as displacements of the spring that can co-occupy space.
Heat and temperature questions
 Metal blocks question
Metal blocks question
The metal blocks question tells students that two metal blocks sitting on a table, one hot and one cold, are placed in contact with one another, and that over the next several minutes, the blocks become the same temperature as one another, and eventually the same temperature as the room. The question asks students what mental model helps them explain why this happens.
Information for instructors:
The metal blocks question is an explain-style question that asks students to apply a model to explain why we observe the behavior described in the question. Our own answer to this question is temperature changes happen when thermal energy moves into or out of an object. When two objects at different temperatures come into contact (such as the two blocks, one hot and one cold, or the hot block and the room), thermal energy transfers until the two objects are the same temperature. (This equilibrium-seeking could be explained in terms of entropy, micro- and macrostates, collisions between particles at the surface of the object, etc.)
Common ideas and sample student responses:
Students used a variety of resources in their responses to this question, including highlighting that temperature changes as a result of thermal energy transfer, naming properties that affect temperature change or thermal energy transfer (e.g., temperature difference, mass or material of objects), citing the Second Law of Thermodynamics, identifying collisions between particles as a mechanism for energy transfer, and evoking a model of a reservoir to explain undetectable changes in temperature (such as in the environment).
For example, one student wrote:
“Heat flows from hot environments to colder environments. So I would think as soon as the cold block touched the hot block heat was transferred to it, and heat from the hot block was being released to the environment via heat waves. So as the heat that is being transferred into the cold block, as soon as the heat enters the cold block it is also emitted into the environment.”
This response draws on a number of resources for understanding thermal phenomena, including the Second Law of Thermodynamics, the idea that thermal energy transfers at contact, and the awareness that multiple objects at different temperature are in contact.
Some students articulated a mechanism for thermal energy transfer at contact. For example:
“There is a transfer of kinetic energy between fast moving molecules (in the hot block) with slow moving molecules (in the cold block). Which facilitates the transfer of having both blocks being the same temperature.”
Here, the student articulates that particles in the hot block will be moving faster than particles in the cold block, such that when the two come into contact, energy will transfer between them.
Students also referenced diffusion and reservoirs, for example:
“The concept of diffusion, hot air will travel to the cold and cold to hot until it reaches equilibrium. The heat in both block will reach back and forth but the room is way bigger, the heat from both block will expand towards the room, but the size of the room is way bigger, both hot and cold waves of temperature would just decrease and increase until it is at an equilibrium with the room temperature.”
This student paints an image of thermal energy exchange and movement through space, where energy travels between objects until equilibrium is reached. They justify the stable temperature of the room in terms of it being big, like a reservoir where thermal energy can spread out such that the temperature change of any one part is negligible.
In the metal blocks question, as with other thermal physics questions we asked, elicited a variety of resources, many of which blended everyday and physics classroom language to predict or explain thermal phenomena. The metal blocks question in particular appears to foreground energy transfers at contact, and equilibrium-seeking, alongside some mechanisms for both.
 Heat transfers from hot to cold question
Heat transfers from hot to cold question
The heat transfers from hot to cold question cites a colloquial version of the Second Law of Thermodynamics – that heat or thermal energy transfers from hot to cold – and asks students how they make sense of this.
Information for instructors:
The format of this is an explain-style question, but the content is somewhat different; rather than asking students to explain the observed behavior of a system, we ask them to say how they make sense of a “rule” they have learned in physics class.
There are a variety of canonically correct answers to this question. Our answer focuses on the microscopic processes: microscopically, hot objects have higher temperatures, which corresponds to particles with higher kinetic energy. When two objects come into contact, one hot and one cold, the interactions between the higher—and lower—energy particles at the point of contact transfer some of the energy to the colder object.
Common ideas and sample student responses:
Students used a variety of resources in their responses to this question. Some responses were tautological–e.g., thermal energy transfers from hot to cold because that’s what thermal energy does–but many responses gave us insight into how students are thinking about thermal energy, equilibrium, and entropy.
Several student responses mimic our microscopic analysis. For example:
“Thermal energy is a result of the movement of the particles so there is no way you could transfer no movement, so the only direction is transferring movement to no movement.”
Though this student is incorrect in suggesting that colder objects have no particle movement at all, this response does name a mechanism for the directionality of thermal energy transfer: collisions between particles moving at different speeds.
Other student responses gave us insight about how they might be thinking about equilibrium (and thus what kinds of activities or analogies might support continued conceptual development). For example, one student wrote:
“Heat transfers from hot items to cold items because of the universe’s ‘need’ for balance. Equilibrium is the most stable state for the universe to be in and that is seen in exchange of heat as well. The hot item’s molecules have more kinetic energy than the molecules of the cold items. Energy can be shared as heat so in order for the two objects to have equal energies, heat flows from the object with higher energy to the object with lower energy.”
This response personifies the universe as having a need for balance and stability, saying that transferring energy from the hot object (whose molecules have more kinetic energy) to the cold one creates the conditions under which the two objects can have equal energies. Other responses referenced “evening out,” “concentration,” and “spreading out.”
Still other responses directly referred to entropy and micro- or macrostates, though these responses were less common. For example:
“Thermal energy transfers from hot to cold objects, and not the other way around because of entropy. Since entropy cannot decrease in a closed system, the system tends toward high entropy. One object having higher temperature than another is a more organized state than both objects being in thermal equilibrium, so thermal energy tends to transfer from hot objects to cold objects.”
This response cites a colloquial definition of entropy as being about the degree of organization of a particular state, saying that the state in which more energy resides in one object is more organized than the state in which objects share the energy equally, and thus the tendency is toward the latter.
In short, the heat transfers from hot to cold question appears to do what it was designed to do, which is to support us (instructors and researchers) in better understanding how students are thinking about the nature of thermal energy transfer, equilibrium, and entropy.
 Particles and cubes what-is-possible questions
Particles and cubes what-is-possible questions
The particles and cubes what-is-possible questions ask students what scenarios are possible as a result of given experimental set-ups. These are explain-style questions that are meant to explore student thinking about statistical probability.
Information for instructors:
Correct answers to the what-is-possible questions depend on the assumptions students make. For example, if three identical cubes are left in boiling water for 5 minutes before their temperatures are measured, the final measured temperature possibilities may differ based on whether the student assumes the cubes have a small number of particles in them or a large (N ~ NA) number of particles. The second law of thermodynamics states that entropy does not decrease, which in tangible terms means that heat flows from hot to cold. For a cube system with a small number of particles, it is possible, however unlikely, for the cubes to end up with slightly different temperatures. The larger the system (or the larger the number of particles), the less likely the system is to stray from equilibrium. The 3 particle system has a higher likelihood of being “off-balance” (having particles with different speeds) than the 3-cube system (where “off-balance” would be defined as having different temperatures).
Common ideas and sample student responses:
This set of questions elicited both conceptual and epistemological resources. We saw a mix of resources related to both probability and predictability. One student stated (in response to “cubes”):
“This doesn't make sense, as temperature wants to equalize, and the water would have to drain energy from one of the cubes, violating the second law of thermodynamics.”
This student demonstrates an understanding that that equilibrium is the most probable state (”temperature wants to equalize”). They also state that the outcome proposed in the question is not possible due to physics laws (”the water would have to drain energy […] violating the second law”), which we interpret as pointing to the student’s thinking about how we know in physics (epistemology).
(In response to “cubes”): “In theory, the energy in the system has the highest probability of being distributed equally to all of the cubes, thus heating them all equally. However, in practice, it is possible for more energy to enter one of the cubes than the others, thus explaining this situation.”
This student uses the resource that energy and temperature are related (”energy […] being distributed equally […] thus heating them all equally”); they also state that the stated outcome is possible, due to the random behavior of particles, but unlikely (”in theory […] highest probability of being distributed equally […] in practice, it is possible for more energy to enter one […] than the others”).
(In response to “particles”): “No, since particles collide elastically, so since all three particles initially had the same speed, they will maintain the same speed.”
This response uses multiple relevant ideas, such as the idea that identical experiments will have identical outcomes (”all three particles initially had the same speed, they will maintain”), an idea more closely tied to predictability than probability. They also draw on the resource that energy and speed are related, but particularly attend to collisions as a mechanism for energy transfer, pointing out that because the collisions are elastic, there is no transfer of energy and therefore no change in speed. (”particles collide elastically, so […] they will maintain the same speed”).
The types of ideas students used in their responses covered a wide range. More importantly, it sheds relevant light on how students think about the possibility of scenarios occurring, and the context-dependence (microscopic particles vs. macroscopic cubes) of their ideas, reasoning, and beliefs about physics.
About
 ACORN Physics Tutorials support learning environments that Attend to Conceptual Resources in Physics. Conceptual resources are potentially generative student ideas: “seeds of science” that can grow toward sophisticated understandings with support and cultivation. ACORN Physics Tutorials support students to construct their own models for physics concepts. Students engage in three main activities as they iteratively build a model they can use to explain and predict phenomena:
ACORN Physics Tutorials support learning environments that Attend to Conceptual Resources in Physics. Conceptual resources are potentially generative student ideas: “seeds of science” that can grow toward sophisticated understandings with support and cultivation. ACORN Physics Tutorials support students to construct their own models for physics concepts. Students engage in three main activities as they iteratively build a model they can use to explain and predict phenomena:
- Gather: Students respond to conceptual physics questions that research has shown to consistently elicit generative student ideas about specific physics topics (e.g., wave propagation, dc circuit behavior, collisions).
- Articulate: Students express their ideas more formally, often as a set of rules.
- Apply: Students apply and test their models for a phenomenon.
 ACORN Physics Tutorials Facilitator Guide
ACORN Physics Tutorials Facilitator Guide
How do I implement ACORN Physics Tutorials?
- Use these tutorials in person or in synchronous online classes in a 50-90 minute period.
- Arrange for students to work on the worksheets collaboratively in groups of 3-4.
- Plan for intermittent but regular instructor engagement with every group: If possible, there should be one instructor for every 2-4 student groups. Near-peer facilitators (LAs or TAs) are helpful.
- Instructors should prepare for both the general approach taken by the worksheet and the specific worksheet questions in a preparation session that takes place before class.
- The worksheet should not be graded, so that students can explore a variety of ideas without feeling pressure to get the right answer.
What should I expect students to do during an ACORN Physics Tutorial, and how can I help?
- Students will generate many novel ideas and questions. Instructors can:
- Notice and elevate their original ideas and questions.
- Revoice their ideas and questions back them.
- Ask clarifying questions to help them connect the dots.
- Students will experience vexation points, “critical moment[s] when they articulate an inconsistency or gap in their understanding that kicks off the sensemaking frame.” (Odden & Russ 2018) Instructors can:
- Suggest analogies, thought experiments, and contrasting cases to support students’ sensemaking process.
- Choose questions or observations to elicit additional conceptual resources that are fruitful for the context. (Particular ideas, representations, or experiments discussed in previous class sessions, etc.)
- Students will be motivated to answer their novel questions, but will find this challenging. Instructors can:
- Suggest ways students can refine their question to be answerable within the scope of the knowledge and equipment they have access to.
- Suggest experiments to test/explore students’ questions.
- Students will wonder whether their ideas are idiosyncratic or shared. Instructors can:
- Encourage students to share ideas with each other.
- Facilitate sharing by asking questions about how students’ ideas connect to one another.
- Connect students’ own ideas or models with canonical models and concepts.
What do students get out of the ACORN Physics Tutorials? What are the specific concepts my students will know after completing an ACORN Physics Tutorial?
Topic-specific instructor guides that answer these questions for each tutorial can be found under the “Materials” tab.
Can I see an ACORN Physics Tutorial in action?
These short video clips and training lessons can give instructors a sense of how students learn with ACORN Physics Tutorials. Watch the short video clips to understand what student might do and discuss, and use the sample discussion prompts to prepare yourself to teach with these Tutorials.
 What enables students to answer their own questions?
What enables students to answer their own questions?
 How do students build new ideas?
How do students build new ideas?
 Should I help students solve problems efficiently?
Should I help students solve problems efficiently?
What materials come with ACORN Physics Tutorials?
- Worksheets for students (editable and pdf)
- Instructor guides, including common student ideas about each physics topic
- Periscope video lessons for instructor training, highlighting how ACORN Physics tutorials elicit student thinking about specific topics and illustrating instructor moves that effectively support students’ progress
How does an ACORN Physics Tutorial work?
ACORN Physics Tutorials guide students through the process of developing a model, or set of rules, that explain observations and make predictions for a particular concept. Small groups of students work through a series of questions to prompt their thinking. Throughout the worksheet, they are asked to keep track of the central ideas and concepts that they use to explain and predict by writing ideas and rules in a model-building box. By the end of the worksheet, each student’s model-building box should contain a self-consistent model that explains the results of the experiments students have analyzed. The goal is for each student to develop a consistent set of rules, not for all students to develop the same set of rules. Rules may be simple or complex.
Example model-building box completed by a student:
|
Model-Building Box: Circuits “Bulbs light up when there is a current going through the bulb. When there is a difference in potential, the positively charged electrons can flow through the bulb with a current that is proportional to the potential difference divided by the resistance of the bulb. The current flows from high to low voltage. This means that the potential difference on either side of the batteries and resistors that are in a circuit is what dictates the direction of current flow for the whole circuit. With this being said, different bulbs within the same circuit can have different levels of brightness due to having different amounts of current flowing through them. In a series circuit with identical batteries and bulbs, the current is equally distributed among all the bulbs. The voltage is based on adding the sum of all the voltages from the batteries and the resistance is based on adding the resistance of each of the bulbs. In a parallel circuit, you could have a wire after a bulb that splits current equally down two different pathways and therefore those two bulbs that are using current that has been split will be dimmer than the first bulb with access to the full current.” |
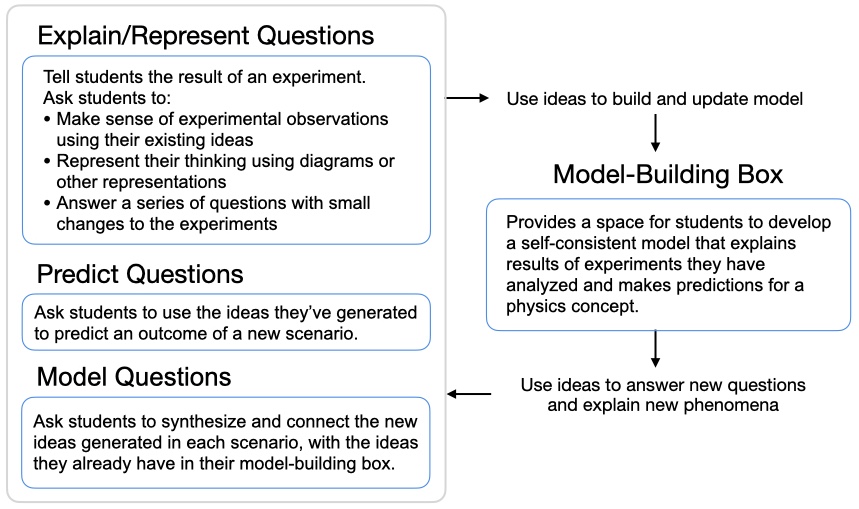
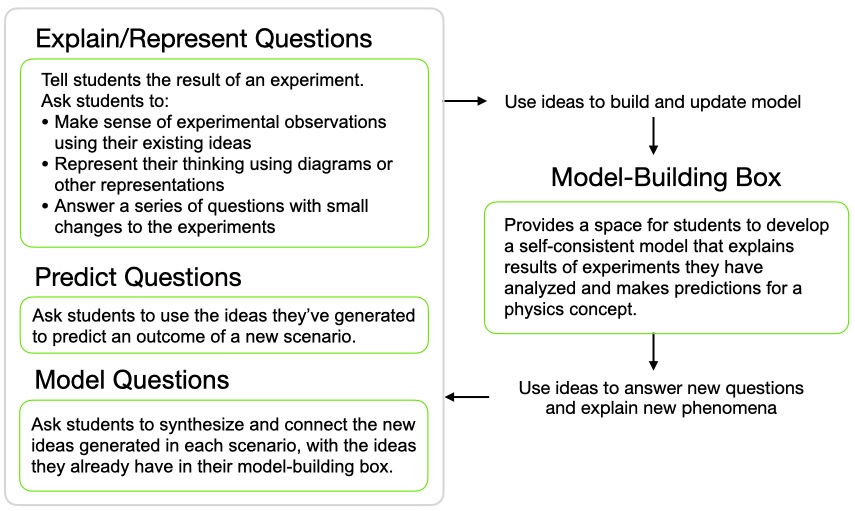
These tutorials ask students three different types of questions:
- Explain/represent questions tell students the result of an experiment or a law of physics and then ask them to generate ideas to explain why that is the result. They may also ask students to represent their thinking—or the phenomenon they’ve just explained—using diagrams or other representations. Students may be given a series of experiments where small changes are made, and asked to generate multiple explanations and refine their ideas based on these.
 These questions elicit students’ ideas about key physics phenomena. Starting with the result rather than a prediction provides opportunities for students to be right and to practice using tools to represent their own thinking. Students’ representations provide opportunities for instructors to quickly visualize how students are thinking.
These questions elicit students’ ideas about key physics phenomena. Starting with the result rather than a prediction provides opportunities for students to be right and to practice using tools to represent their own thinking. Students’ representations provide opportunities for instructors to quickly visualize how students are thinking.
- Predict questions ask students to use the ideas they’ve generated so far to predict an outcome of a new scenario. Students are not asked to predict until they are likely to have enough of a model to predict correctly.
 These questions give students practice applying their model and make visible places where the model needs to be refined.
These questions give students practice applying their model and make visible places where the model needs to be refined.
- Model questions ask students to synthesize and connect the particular ideas they have been working with, with the ideas they have in their model-building box.
These questions guide students toward a consistent conceptual model for the set of phenomena presented in the worksheet.
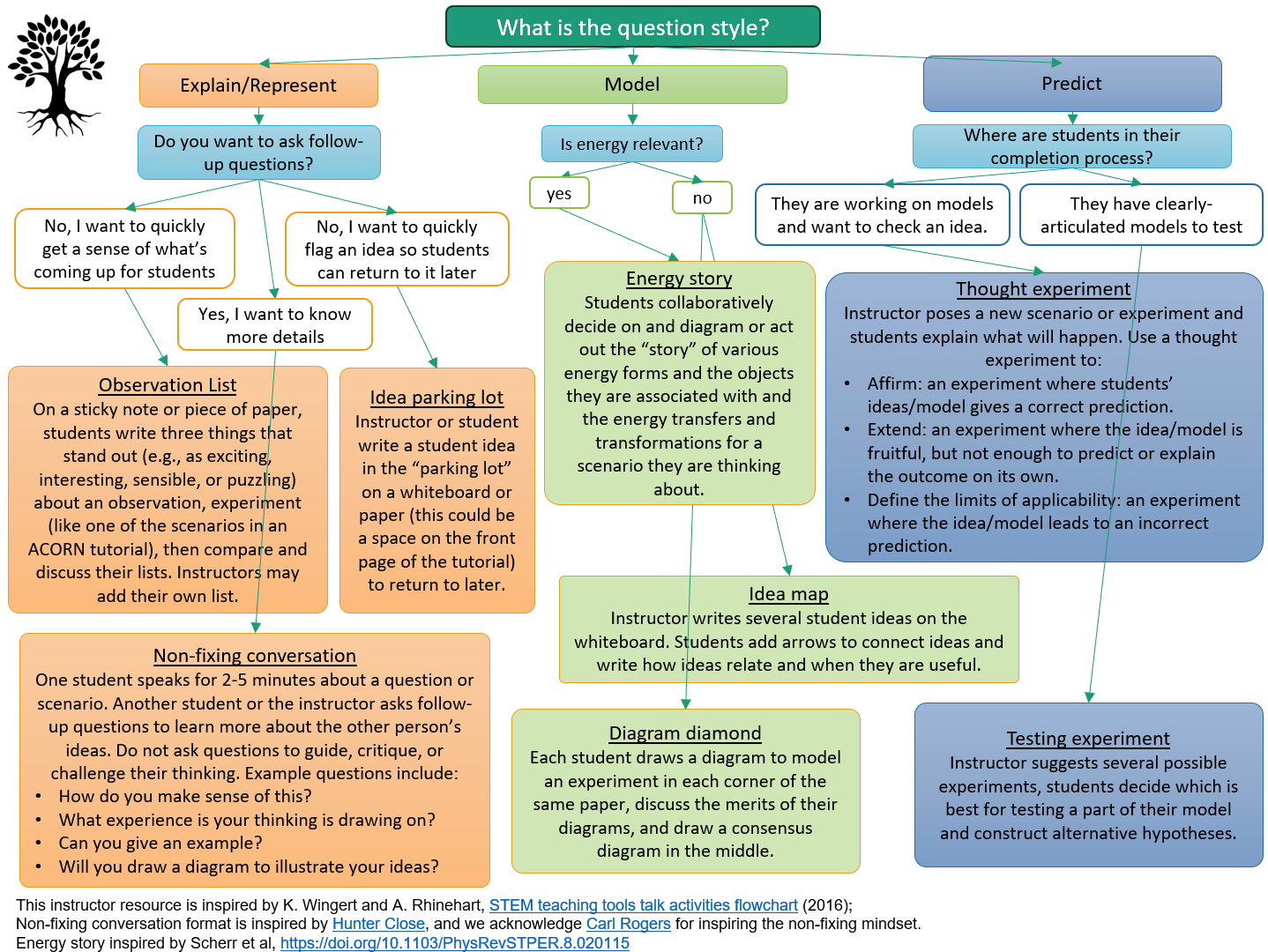
What do I do to help students as they work through the Tutorials?
This talk moves flow chart outlines strategies for instructors to use to understand and nurture students’ ideas for each type of question in ACORN Physics Tutorials:
How do I integrate ACORN Physics Tutorials with other teaching materials?
ACORN Physics Tutorials are meant to be integrated with other teaching materials (including materials developed by instructors and other research-based instructional materials), and our development team encourages instructors to do this in the way that makes most sense for their unique classrooms. In our own introductory physics courses, we have used ACORN Physics Tutorials in place of other research-based physics worksheets Often we follow up an ACORN Physics Tutorial with a selection of questions or another worksheet from another set of teaching materials that builds on the ideas students developed in the ACORN Physics Tutorial.
How long does it take for students to complete an ACORN Physics Tutorial?
ACORN Physics Tutorials are designed to be used in a single 50-90 minute class session. The time it takes a group of students to complete a worksheet can depend on how much experimentation and sensemaking the group pursues and how much instructional support is available (e.g., TAs or LAs). In longer class sessions, students are likely to have time to consider some follow-up challenge problems (chosen by the instructor), while in shorter class sessions challenge questions can be given on homework and/or in a subsequent lecture.
Where do I find the answer keys for the ACORN Physics Tutorial questions?
We do not provide answer keys to ACORN Physics Tutorials because most of the questions in each Tutorial are open-ended and have more than one correct (or productive, even if incomplete or incorrect) answer. ACORN Physics Tutorials are designed to elicit a variety of responses to each question, and instructors' attention to this variety is important for accomplishing the learning goals of each tutorial. The purpose of ACORN Physics Tutorials is to leverage students’ own ideas, and instructors should support students to test and refine their own answers using experiments, counterexamples, and scientific argumentation amongst peers. You can find example student responses to some key questions in each ACORN Physics Tutorial under the “Conceptual Questions” tab and example models that students have articulated after doing the Tutorials in the Instructor Guide for each Tutorial (available on the individual Tutorial page).
 FAQs
FAQs
How are ACORN Physics Tutorials different from other research-based tutorials?
Like other research-based instructional strategies in physics, ACORN Physics Tutorials are based on common student ideas about specific physics topics, and have been tested and validated in undergraduate physics classrooms. (for more information about our team’s research on common student ideas and testing of ACORN Physics Tutorials, visit the Research page).
Unlike some research-based instructional strategies, ACORN Physics Tutorials are designed to target students’ common fruitful ideas about physics phenomena, rather than common difficulties or misconceptions. ACORN Physics Tutorials are also designed to prioritize sensemaking around students’ emerging ideas, experimentation, and scientific model building, rather than tightly-specified content learning goals. The table below highlights some of these differences:
|
ACORN Physics Tutorials |
Difficulties- or misconceptions-based Physics Tutorials |
|
Based on research about student understanding of physics |
|
|
Support students in building models of physics concepts |
|
|
Improve students’ conceptual understanding of physics |
|
|
Designed to help students build models and engage in sense-making about physics, often by asking students to use their own good ideas as “seeds of science” and build on them. |
Designed to help students build correct models of physics, often by eliciting their misunderstandings about physics and helping them confront and resolve them. |
|
Instructor guides help you notice student seeds of science as they come up and decide what you might do next. |
Instructor guides help you understand what misunderstandings students might have and how to address them. |
|
Students can learn that they have good ideas and can engage in sense-making about science, but some students may be frustrated by the open-ended nature of the activities and the lack of a satisfying conclusion. |
Students can learn that the activities will help them get correct answers, but some students may conclude that their intuitions and initial ideas about physics are often wrong. |
Why should I use ACORN Physics Tutorials in my class, instead of what I am currently using?
ACORN Physics Tutorials may be a great option for your introductory physics class if you are looking:
- To facilitate more student-directed sensemaking and encourage students to engage in the process of building a scientific model of their own. ACORN Physics Tutorials can support sensemaking and model building with open-ended scaffolding for student inquiry and discussion.
- For flexible, adaptable instructional materials that can be integrated with physics simulations, experiments, or demonstrations. ACORN Physics Tutorials are designed to facilitate student-directed experimentation with simulations (such as PhET simulations) and hands-on experiments.
- To incorporate more teaching practices that encourage students’ agency; highlight the fruitful ideas in students’ own thinking; and facilitate frequent, responsive formative assessment.
Are there more ACORN Physics Tutorials under development?
We are not currently developing more ACORN Physics Tutorials. However, it is our goal that the existing Tutorials, along with the information provided in the facilitator guide, can be used as a model for instructors to make their own ACORN-like instructional materials for other topics. For more information about our design process and strategies, see “How does an ACORN Physics Tutorial work?” in the Facilitator Guide above.
Do students like working through the ACORN Physics Tutorials?
In general, we find that students experience excitement, frustration, and have “aha! moments,” like they do when learning with other small-group activities or tutorials. ACORN Physics Tutorials encourage experimentation (often virtually with simulations like PhET Interactive Simulations), which students often find fun and rewarding.
Have questions about ACORN Physics Tutorials? Contact Amy Robertson.
People
Current Team Members
 |
Amy Robertson (she/her, PI, Seattle Pacific University) is a Research Professor and physics education researcher with a strong interest in cultivating liberatory classroom and professional spaces. In her work, Amy roots herself in a variety of methodological tools, disciplinary and interdisciplinary collaborations, and her lived experience as a disabled and chronically ill physicist. Her research focuses on university students’ conceptual resources for learning physics and how frameworks from equity and justice can help physicists become more critically conscious. She is a proud puppy mama, a disabled hiker, and an avid crafter. |
 |
Paula Heron (she/her, PI, University of Washington) is a Professor of Physics at the University of Washington. She has been engaged in physics education research with a focus on improving student conceptual understanding and reasoning ability for nearly 30 years. She is involved in a number of international organizations and collaborations in PER and has been recognized by awards from the American Physical Society and the American Association of Physics Teachers. Dr. Heron is an Associate Editor of Physical Review Physics Education Research. |
 |
Rachel Scherr (she/her, co-PI, University of Washington) is an Assistant Professor of Physics at the University of Washington Bothell. A longtime physics education researcher, she has a special interest in educator development, including physics faculty, K-12 teachers, graduate teaching assistants, and undergraduate learning assistants. Dr. Scherr is the producer of Periscope Video Lessons. |
| Raphael Mondesir (he/his, co-PI, Seattle Pacific University) is an Assistant Professor of Sociology at Seattle Pacific University. As a quantitative sociologist, Dr. Mondesir utilizes a variety of methods to study the intersection of community development, civic participation, and religious pluralism in the Global South. His special interest in civic cultures and social networks often inform his teaching and how he builds relationships with his students. Dr. Mondesir spends his weekends playing soccer or hiking. | |
 |
Lisa Goodhew (she/her) is an Assistant Professor of Physics at Seattle Pacific University. Her research focuses on university students’ conceptual resources for understanding physics and supporting instructors in effectively leveraging these resources. Dr. Goodhew’s favorite part of her work is getting to know and learn with students in and out of the physics classroom, and she is excited by the ways this research makes her a better teacher. |
 |
Lauren Bauman (she/her) is a research coordinator at the University of Washington Seattle. She first became interested in physics education research while learning physics as an undergraduate and is particularly interested in effectively creating empowering, equitable, and supportive educational spaces that authentically center students' ideas. Most of her research focuses on analyzing written data to identify students' conceptual resources. |
 |
Anne Alesandrini (they/them and she/her) is a current graduate student with the Physics Education Group at the University of Washington and a former public high school teacher. Their research interests include student explanations and educator development, and they spend a lot of time thinking about the interactions between education, science, and society. They find joy wandering around outside with their kids looking at plants. |
 |
Al Snow (they/them) is a graduate student in Physics at the University of Washington. They are currently working on classroom discussion video analysis and pretest response analysis. Al enjoys reading and writing, as well as listening to and performing music. |
 |
Sam McKagan (she/her) is the creator and director of PhysPort, a website that supports physics faculty in research-based teaching and hosts open-source curricular materials, including the ACORN Tutorials. She has conducted research into physics faculty members’ and department heads’ needs around research-based teaching and assessment, and conducted several meta-analyses of the impact of research-based teaching in physics. For this project, Sam worked with Adrian to design the ACORNS Tutorials website on PhysPort, and helped analyze interviews with faculty. |
 |
Adrian Madsen (she/her) is the assistant director of PhysPort, a website that supports physics faculty in research-based teaching and hosts open-source curricular materials, including the ACORN Tutorials. She has conducted research into physics faculty members’ and department heads’ needs around research-based teaching and assessment, and conducted several meta-analyses of the impact of research-based teaching in physics. For this project, Adrian worked with Sam to design the ACORNS Tutorials website on PhysPort, and helped analyze interviews with faculty. |
Team Alumni
 |
Yohannes M. Abraham (he/him) is a former undergraduate cellular and molecular biology student at Seattle Pacific University interested in STEM teaching and learning as well as the medical field. He joined physics research to better understand why students’ have common conceptual misconceptions about physics and how to address these difficulties with a resource-oriented teaching and learning approach. He plans to work in a biology laboratory and wishes to attend medical school in the future. During his free time, he loves to play soccer, try different cuisines, and read Italian classic books. |
| Cheyenne Broadfoot is a graduate from University of Washington Bothell with a B.S. in Physics and is currently pursuing a M.S. in Coastal Zone Management and Marine Conservation from University of Miami Rosenstiel School of Marine and Atmospheric Science. She has a passion for learning and wants to use the acquired knowledge to work for an organization addressing wastewater and pollution in third world countries, specifically Costa Rica. | |
 |
Beth Gallatin is a former undergraduate student at South Puget Sound Community College studying computer science. She joined the physics education research project to help develop a deeper understanding of students' conceptual resources and begin exploring strategies to create a more inclusive and diverse society of physicists. She is currently participating in research for the LIGO Collaboration working on the search for continuous wave gravitational radiation. She loves thinking and wondering about gravity, and the role it plays in our understanding of the universe. She has a persistently curious mind, and plans to focus on a career that bridges scientific resources, nature, and humanity. |
 |
Jon Geiger is a graduate of Seattle Pacific University, where he received degrees in Physics, Applied Mathematics, and Honors Liberal Arts. He served as a Learning Assistant for three years, and has worked with the team on a project investigating the utility of natural language processing in characterizing students’ conceptual resources in physics. |
 |
Brynna Hansen is a former undergraduate student studying Cellular and Molecular Biology at Seattle Pacific University, and does physics education research as a side hobby! She hopes to attend medical school following graduation. Outside of school Brynna loves to read, exercise and spend time with loved ones. |
 |
Tra Huynh (she/her) is a former postdoctoral scholar at University of Washington Bothell. She is a physics education researcher and she has been conducting qualitative research on faculty and student professional development and equity education through multiple lenses of methodology and theories. She loves creating ideas with people and turning them into research. She is an aspiring knitter and baker. |
 |
Katie Marvin is a graduate of UW Bothell with a BS in physics. Before becoming a student, she was a dog trainer who taught large classes to the general public. Her experience in behavioral training, communication, and observation served her well as she worked her way through an associate's degree at South Seattle College. These same skills would prove useful when she was encouraged to join the physics education research project for her independent research credits. She has a passion for learning, teaching, and bringing out the best in others. After graduating she landed a job within the semiconductor industry. She plans to become a physics instructor someday after she has gained some real world application experience. With the free time she has, she likes to practice her woodwind instruments, hike, play retro games, and hang out with her dog, Zac. |
 |
Clausell Mathis is a former postdoctoral scholar in physics at the University of Washington - Seattle. Clausell has been engaging in physics education research over the past 4 years with a focus on understanding how physics instructors can incorporate culture-based equitable approaches to teaching from a curriculum development, student learning, and teacher identity lens. |
 |
Jon Owen (he/him) is a former undergraduate student in physics at Seattle Pacific University. He is works to analyze videos of classrooms using ACORN Physics tutorials to understand how students’ conceptual resources are activated and refined. |
|
Olin Sorby is a former Undergraduate student studying Applied Physics and Norwegian language at the University of Washington. He worked with Tra on identifying conceptual resources in kinematics, pertaining to productive use of force reasoning in kinematics problems. |
|
 |
Marcella Su (she/her) is a graduate of the University of Washington Bothell with a B.S in Biochemistry and a minor in Health Studies. She is pursuing medicine to become a doctor. She believes that research is essential to medicine in order to propel the field of medicine to create effective treatments for the members of our community. She hopes to practice and provide quality care for her community after medical school, as closing the gap between ethnic and marginalized groups is a core passion of hers. She is currently a Research Assistant at Veterans Affairs, Seattle Epidemiologic Research and Information Center. During her time off she helps her family in residential housing management, volunteers at International District Emergency Center, located in Seattle’s Chinatown, and does sewing with a sewing machine to help tailor clothing for family and friends. |
 |
Andrea Wooley (she/her) is a former undergraduate physics student at Western Washington University with experience in physics education research and Mossbauer spectroscopy. The culture of physics is central to her research interests, in particular she is passionate about issues about justice, equity, inclusion and diversity. She’s a transfer student from South Seattle College where she studied students’ perspectives of physics in addition to working as a tutor and peer navigator. She spends her weekends hiking in Larabee state park, playing pool and taking care of her house rabbit, Monty. |
Research
ACORN Physics Tutorials are developed iteratively, in conversation with research:
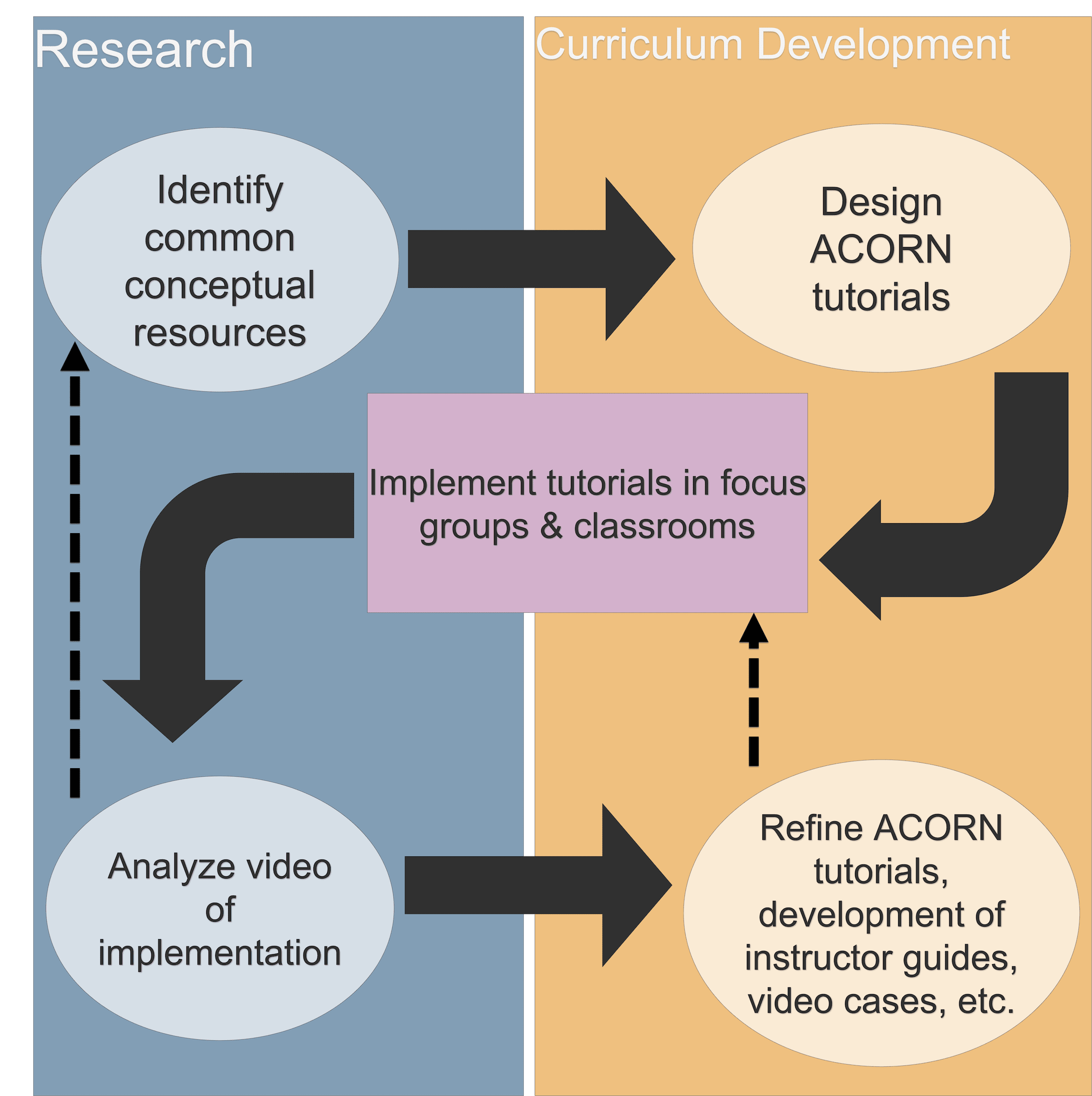
Researchers from our team first use student written responses to conceptual questions to identify specific, common conceptual resources for understanding a particular topic. This research shapes the initial design of an ACORN Physics Tutorial, which elicits and then builds from identified conceptual resources, toward models, mechanisms, and concepts. These tutorials are then implemented in focus groups or classrooms, where students are video-recorded as they learn. Video analysis identifies ways in which the tutorial is working or not working as planned – or working well in unexpected ways – and this analysis then shapes the refinement of the materials. Often materials iterate through this process multiple times before being shared more broadly.
Research identifying students’ conceptual resources for understanding physics
Kinematics
- T. Huynh, A. Alesandrini, L. Bauman, O. Sorby, and A. Robertson, Drawing on force ideas for kinematic reasoning in introductory physics, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- C. Broadfoot, B. Hansen, A. Robertson, and L. Goodhew, Identifying student resources for understanding kinematics, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
Forces
- T. Huynh, A. Alesandrini, L. Bauman, O. Sorby, and A. Robertson, Drawing on force ideas for kinematic reasoning in introductory physics, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- A. Robertson, L. Goodhew, R. Scherr, and P. Heron, University student conceptual resources for understanding forces, Phys. Rev. Phys. Educ. Res. 17 (1), 010121 (2021).
Linear Momentum
- B. Hansen, L. Bauman, Y. Abraham, M. Valentin, and A. Robertson, Identifying student resources for understanding linear momentum, presented at the Physics Education Research Conference 2021, Virtual Conference, 2021.
Energy
- H. Sabo, L. Goodhew, and A. Robertson, University student conceptual resources for understanding energy, Phys. Rev. Phys. Educ. Res. 12 (1), 010126 (2016).
Circuits
- L. Bauman, T. Huynh, and A. Robertson, Substance-based and sequential reasoning about current: An example from a bulb-ranking task using a resources theoretical lens, Phys. Rev. Phys. Educ. Res. 20 (1) 010124 (2024).
- L. Bauman, B. Hansen, L. Goodhew, and A. Robertson, Student conceptual resources for understanding electric circuits, Phys. Rev. Phys. Educ. Res. 20 (2) 020128 (2024).
- L. Bauman, J. Corcoran, L. Goodhew, and A. Robertson, Identifying student conceptual resources for understanding electric current, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
Waves
- L. Bauman, L. Goodhew, and A. Robertson, Students’ use of conceptual resources for understanding superposition, presented at the Physics Education Research Conference 2019, Provo, UT, 2019.
- L. Goodhew, A. Robertson, P. Heron, and R. Scherr, Student conceptual resources for understanding mechanical wave propagation, Phys. Rev. Phys. Educ. Res. 15 (2), 020127 (2019).
- A. Robertson, L. Goodhew, P. Heron, and R. Scherr, Pulses as not-objects: student responses to a new question about the superposition of mechanical waves, Phys. Educ. 54 (5), 055023 (2019).
Heat and Temperature
- A. Alesandrini, T. Huynh, L. Bauman, and A. Robertson, Identifying student resources for reasoning microscopically about heat and temperature, presented at the Physics Education Research Conference 2022, Grand Rapids, MI, 2022.
- Y. Abraham, M. Valentin, B. Hansen, L. Bauman, and A. Robertson, Exploring student conceptual resources about heat and temperature, presented at the Physics Education Research Conference 2021, Virtual Conference, 2021.
Research analyzing implementation of ACORN Tutorials
- L. Bauman, L. Goodhew, A. Alesandrini, A. Snow, and A. Robertson, Shifts in students’ responses to conceptual questions after a new physics conceptual worksheet: Preliminary findings, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- A. Robertson, L. Bauman, Y. Abraham, B. Hansen, H. Tran, and L. Goodhew, Resources-oriented instruction: What does it mean, and what might it look like?, Am. J. Phys. 90 (7), 529 (2022).
- L. Goodhew, A. Robertson, and P. Heron, A case of resources-oriented instruction in calculus-based introductory physics, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
Related research by the development team
- J. Owen, L. Goodhew, and B. Hansen, "Which has more energy?" - An example of responsive teaching in university physics, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- A. Robertson, L. Goodhew, L. Bauman, B. Hansen, and A. Alesandrini, Identifying student conceptual resources for understanding physics: A practical guide for researchers, Phys. Rev. Phys. Educ. Res. 19 (2), 020138 (2023).
- A. Snow, P. Heron, L. Bauman, A. Robertson, and L. Goodhew, A case in which canonically incorrect ideas do not hinder conceptual progress in introductory physics, presented at the Physics Education Research Conference 2023, Sacramento, CA, 2023.
- J. Geiger, L. Goodhew, and T. Odden, Developing a natural language processing approach for analyzing student ideas in calculus-based introductory physics, presented at the Physics Education Research Conference 2022, Grand Rapids, MI, 2022.
- A. Robertson, L. Goodhew, P. Heron, and R. Scherr, Impetus-Force-Like Drawings May Be Less Common Than You Think, Phys. Teach. 60 (4), 254 (2022).
- L. Bauman, C. Mathis, S. McKagan, A. Madsen, K. Marvin, L. Goodhew, and A. Robertson, Centering physics faculty ideas about resources-oriented instruction, presented at the Physics Education Research Conference 2021, Virtual Conference, 2021.
- L. Goodhew, A. Robertson, P. Heron, and R. Scherr, Students’ context-sensitive use of conceptual resources: A pattern across different styles of question about mechanical waves, Phys. Rev. Phys. Educ. Res. 17 (1), 010137 (2021).
- A. Robertson, L. Goodhew, R. Scherr, and P. Heron, Impetus-Like Reasoning as Continuous with Newtonian Physics, Phys. Teach. 59 (3), 185 (2021).
- R. Mondesir and A. Robertson, Toward characterizing the demographics of introductory physics courses, presented at the Physics Education Research Conference 2020, Virtual Conference, 2020.
- L. Goodhew, A. Robertson, P. Heron, and R. Scherr, Examining the productiveness of student resources in a problem-solving interview, presented at the Physics Education Research Conference 2018, Washington, DC, 2018.
A pedagogy course to support resources-oriented instruction

Rachel E. Scherr (University of Washington Bothell) and Lisa M. Goodhew (Seattle Pacific University)
These materials are suitable for a pedagogy course to support learning assistants (LAs) and teaching assistants (TAs) in using resources-oriented instruction. We suggest weekly readings, weekly reflections, one project per term, and one peer observation per term.
 Background
Background
Nationally, student instructional assistants play an important role in undergraduate STEM education. Graduate and undergraduate students help STEM faculty make their courses more interactive, especially by facilitating small-group interactions in large classes. (At UWB and SPU, these instructional assistants are all undergraduates, and are called “peer facilitators” (UWB) or “learning assistants” (SPU).) Student instructional assistants not only improve the quality of instruction for their students, but also enhance their own educational experience with a low-stakes, high-access, early teaching experience, and are recruited into the teaching profession.
The instructional assistants’ experience is at its best when it includes a pedagogy course, in which their experiential learning in classrooms is enriched by learning about the big ideas of STEM teaching and learning. At UWB, undergraduate physics peer facilitators who take a pedagogy course have been struck by the difference it made to them: one reflected, “In the beginning, I had never considered using open questions to promote discussion and freedom to speculate and share ideas, which I now know is how students have their ‘aha’ moments. I now try to figure out student’s mental models and create my advice and help based on that.” Pedagogy courses also provide “stealth” professional development to the faculty that supervise them, engaging them in insightful discussions about best-practices teaching and learning that support reflection on their own practices.
In pedagogy courses around the US, instructional assistants read education literature and engage in activities and discussions to deepen their understanding of best practices teaching and learning. As part of the Conceptual Resources project, we are developing a pedagogy course that will support resources-oriented instruction: one that will support instructional assistants to see student ideas in terms of productive resources, and teach them to support students in recognizing and building on each others’ scientific ideas. The primary learning goals for the course are for instructional assistants to develop both an appropriate learning theory and practical skills:
- Instructional assistants should be able to (A) explain the teaching benefit of detecting and interpreting students’ physics ideas, and (B) develop practical strategies for bringing out and building on students’ ideas.
- Instructional assistants should be able to (A) explain the learning benefits of collaborative work, and (B) support students in understanding and building on each other’s ideas.
These learning goals are a long way from where most instructional assistants begin. One learning assistant expressed a common starting point: “I think that being an LA means our job is to carefully guide the students through the material... I hope to accomplish communicating these physical ideas well enough to the students that the ideas are ingrained into them.” The shift from “explainers” to facilitators who know how to elicit, interpret, and respond to student thinking is significant for many instructional assistants, in some cases transforming their view of their own educational experiences.
A high-quality pedagogy course is especially important in this project because early evidence indicates that students’ experience of their own ideas as valuable and potentially fruitful may depend more on how the resources-oriented instructional materials are implemented than the materials themselves. Our pilot tests of resources-oriented worksheets on wave propagation and circuits featured numerous instances in which students generated sophisticated scientific questions or models, and were at the same time frustrated by their lack of “right answers.” One group put it this way:
Jian: That was… very laid back and stressful at the same time.
Wendy: Yeah.
Jian: Like I just gotta know—
Wendy: Yeah, that’s how tutorial will be!
Paige: I don’t do well with not having clear answers about things. I just need to know.
Jian: I’m like come on tell me! Or at least help me understand.
Paige: I think we were supposed to be made more comfortable with uncertainty — which I am not happy about!
In many instances of frustration, an instructor’s (professor, TA, or LA) guidance was significant for the progress of students’ thinking. In some interactions, the instructors’ guidance either confused students further or affirmed notions that there was no real merit to the activity. In other instances, conversation with an instructor helped students to navigate their uncertainty in productive ways or supported students in answering their own questions in ways that refined and extended their understanding. This leads us to think that effective instructor preparation is important for successful implementation of resources-oriented instruction. In particular, our preliminary evidence suggests that resources-oriented instruction is supported by a commitment to understanding and building from student thinking and by flexibly deployed knowledge of scientific concepts and practices.
 Outline of course activities
Outline of course activities
Typical class session
|
First 15 minutes: Each Learning Assistant shares a high and low of each peer assistant’s week of teaching, followed by reflection about why this may have happened and what to take away. LAs might offer each other advice and empathy, and Pedagogy course instructor might offer encouragement, suggestions, or design a future lesson to address an LA’s concern |
|
|
30-40 minutes, as class time allows: [Option A] Group discussion of a reading assignment (see sample course schedules below for suggested reading assignments). |
[Option B] Activity such as “Listening three ways,” the “Non-fixing interview,” or discussion of a Periscope episode. The following Periscope lessons examine students working through ACORN tutorials and highlight questions that are particularly important for teaching with ACORN tutorials: How do students build new ideas? What enables students to answer their own questions? Should I help students solve problems efficiently? |
|
Last 5 minutes: Each Learning Assistant shares one takeaway from this week’s class that they will try out in their teaching next week. |
|
Sample Course Schedule & Learning Goals
|
Wk |
Learning goals |
In-class activity highlights |
Reading and reflection (homework assignments) |
|
1 |
Anticipate a variety of different ways students might explain a physics concept Explain how results of cognitive science are relevant to how students learn (physics) |
Observe different ways students explain a physics concept. Periscope: What ideas do students have about momentum?” Develop strategies for eliciting/supporting multiple perspectives. How can I promote equitable sensemaking by setting expectations for multiple perspectives? |
Reading: Scherr & Redish, "Newton's Zeroth Law: Learning from listening to our students" Reflection: Describe a student interaction that gave you insight into the student's mental model and/or prior knowledge about a physics concept. |
|
2 |
Periscope: What ideas do students have about mechanical energy? |
Reading: Redish, "Implications of cognitive science for teaching physics" Reflection: Come up with as many ways as you can to answer the following physics question [choose one]. |
|
|
3 |
Recognize and describe the “disciplinary substance” of students’ ideas Explain the teaching benefit of seeing students’ ideas in terms of productive resources |
Periscope: How can I bring out students’ ideas? Discuss Sean numbers Introduce formative assessment + the formative assessment cycle |
Reading: Blosser, “Ask The Right Questions” Reflection: Share some teacher questions that you remember from recent interactions: either questions you asked when you were teaching, or questions that a teacher asked you. What type of question is it? What is its function? What does it say about the kind of teaching that is happening? |
|
4 |
Non-fixing interview - practice in class |
Reading: Hammer, “Student resources for learning introductory physics” Reflection: Reflect on a time in your teaching where you noticed a student had a misconception or wrong idea. How did you respond? Could that idea have been fruitful in another situation? |
|
|
5 |
Plan questions and activities to respond to / build on students’ scientific ideas Explain the teaching benefit of detecting and interpreting students’ physics ideas |
Final project discussion and planning |
Reflection: Reflect on a time in your teaching where you noticed a student had a productive idea, even if it wasn’t totally correct. How did you respond? How could that idea be fruitful for the student’s learning? |
|
Periscope: Will students engage in evidence-based argumentation? |
Reflection: How can students/ instructors cultivate a classroom learning community where everyone gets to show their expertise, and where their resources are welcome contributions? |
||
|
7 |
Develop practices for facilitating productive group dynamics/discussions Explain multiple different theories and frameworks for how people teach and learn Develop and practice strategies for fostering an inclusive and equitable learning environment |
Discuss ACORN talk moves flowchart |
Reflection: Describe a time in your teaching where you used a specific talk move? How did it go? |
|
8 |
Analyze cultural displays of science knowledge, such as hip hop physics |
Reflection: Reflect on your teaching interactions now as compared to the start of the quarter. What have you gotten better at over the past several weeks? |
|
|
9 |
Final project presentations: “Non-fixing interview” (Interview a single person to learn about their ideas about a physics concept. Do not teach them anything.) |
||
|
10 |
|||
Growth Mindset & Equitable Group Work
|
Wk |
Learning goals |
Activity highlights |
Reading and reflection |
|
1 |
Explain the teaching/learning benefit of collaborative work Explain the inequities that arise in an unstructured learning environment |
Apple bridge design challenge |
Reading: Mazur video - Peer Instruction for Active Learning Reflection: How do you think group work is helpful for students? Do you think it’s helpful for all students? |
|
2 |
Periscope: If you disagree or How do students build new ideas? |
Reading: Woolley, "Evidence for a collective intelligence factor in the performance of human groups" and "What makes a team smarter?" Reflection: Describe an experience you have had with collective intelligence of a group that you have been in. |
|
|
3 |
Support students in understanding and building on each other’s ideas Describe techniques that add structure and equity to a classroom |
Discuss group roles, referring to Group Roles and POGIL role cards traditional roles |
Reading: Sathy & Hogan article “How to make your teaching more inclusive” Reflection: What is your best skill as a group member? What skill do you think you should work on as a group member? |
|
4 |
Reading: Dweck, Boosting Achievement With Messages That Motivate Reflection: Have you thought that there is a “physics brain” or that someone can be a “physics person”? What attributes did (do) you associate with being a “physics person”? |
||
|
5 |
Explain fixed and growth mindset and their relevance for teaching physics How to interact with students so that all get to speak Know when to step in vs. let students keep going on their own |
Periscope: Do students have the right to be told whether they are correct? Periscope: Should I help students solve problems efficiently? |
Reading: Leslie et al. - 2015 - Expectations of brilliance underlie gender distributions across academic disciplines, Little, Proudness Reflection: What evidence of fixed or growth mindset have you already observed this term? |
|
6 |
What inclines students not to speak? Periscope: How can I bring out student ideas? or Moving box |
Reading: Scherr, Fixed and growth mindsets in physics graduate admissions Reflection: How do you decide to start interacting with a group of students? |
|
|
7 |
How do you decide to start interacting with a group of students, and what does that have to do with fixed vs. growth mindset? Take a statement from the article and turn it into a growth mindset statement. Make a fixed-mindset statement about yourself and turn it into a growth mindset statement. |
Reading: Dweck, “Carol Dweck revisits the ‘Growth Mindset’” Reflection: If you could go back in time and give your students some advice at the beginning of the term (or the year), what would it be? Why? |
|
|
8 |
Describe techniques for supporting a growth mindset in physics teaching Being a good intellectual leader/coach in a group even if you don’t know the answer yourself |
Periscope: How does teaching shape a person’s self-image? or How should instructors handle their own mistakes? |
(no reading) Reflection: Beyond your development as a PF/LA, we are also interested in your development as a student and as a person. To what extent have the topics discussed in this course been useful beyond your PF/LA experience? |
|
9 |
Final project: Analyze an excerpt of yourself teaching (students video- or audio-record themselves teaching, and choose a 2-3 minute clip to analyze and reflect on. See “Record yourself” under Projects below.) |
||
|
10 |
|||
Files
-
Download the ACORN talk moves flowchart:

A one-page handout for instructors with ideas for questions to ask students to prompt their thinking while working on ACORN Physics Tutorials -
Download the Listening three ways:

Handout for a class activity to support LAs in listening more effectively -
Download the Non-fixing interview:

Handout for a class activity to support LAs in deeply understanding someone else's ideas
 Readings
Readings
Readings for LAs to learn about conceptual resources
Student resources for learning introductory physics
Misconceptions Reconceived: A Constructivist Analysis of Knowledge in Transition
Discovery Learning and Discovery Teaching: Cognition and Instruction
Implications of cognitive studies for teaching physics
Newton's Zeroth Law: Learning from Listening to Our Students
Attending and Responding to Student Thinking in Science
"Charges are everywhere": A case of student sensemaking about electric current
Examining the productiveness of student resources in a problem-solving interview
Other readings that support a resources orientation
Boosting Achievement with Messages that Motivate
Expectations of brilliance underlie gender distributions across academic disciplines
Evidence for a Collective Intelligence Factor in the Performance of Human Groups
G: The Miseducation of Larry P
Why Peer Discussion Improves Student Performance on In-Class Concept Questions
 Reflections
Reflections
Reflection is a key practice for integrating experience. In general, we suggest that satisfactory teaching reflections must do the following:
- Be posted on time
- Consist of at least 300 words OR two minutes of video
- Demonstrate that you have read the course material
- Be accurate about the course material
- Draw explicit connections between ideas raised in the readings to teaching or learning experiences you have had
- Convey something that personally struck you as interesting, compelling, engaging, or otherwise moved you
- Write or speak in a clear manner – your style can be less formal than typical academic prose, but it should be serious and engaged with ideas
Reflection prompts
Identify one ‘take-away’ related to how you will respond to students’ contributions this term. What will you commit to try out in your practice to shift deeper into an asset-based view of sense-making? ("Asset-based" means you think of students' ideas as being valuable, instead of wrong or absent; it is the opposite of "deficit-based.") A possible prompt: “In order to__________, I will work to_______. I will know I am making progress if__________."
Why do you think groups are effective for learning? You may refer to the course you are helping teach or your own experience as a student.
What is your best skill as a group member? What skill do you think you should work on as a group member?
Describe an experience you have had with “collective intelligence” of a group that you have been in.
How do you decide to start interacting with a group of students?
Have you thought that there is a “physics brain” or that someone can be a “physics person”? What attributes did (do) you associate with being a “physics person”? How might this affect how someone participates in a physics class?
What evidence of fixed or growth mindset have you observed this term? This could come from working with students, reflecting on your own mindset, or observing other instructors.
Share some teacher questions that you remember from recent interactions: either questions you asked when you were teaching, or questions that a teacher asked you. What type of question is it? What is its function? What does it say about the kind of teaching that is happening?
How do you know someone has learned something? You can’t see into their head. Think of someone you know who has a lot of expertise in some area, and it’s not the kind of thing where you take a test. How does their expertise show?
Describe a time when you had a feeling of learning, but later realized that your learning was not as high-quality as it felt at the time; or when you felt like you were not learning, but later realized your learning had been deeper than you realized.
Describe a teaching experience you had recently that felt successful to you. What about it felt successful? Describe a teaching experience you had recently that felt less successful to you. What leads you to see it this way?
How can students/ instructors cultivate a classroom learning community where everyone gets to show their expertise, and where their resources are welcome contributions?
Describe a student interaction that gave you insight into the student's mental model and/or prior knowledge about a physics concept.
If you could go back in time and give your students some advice at the beginning of the term (or the year), what would it be? Why?
If you have a future career or other life goal, how is being an LA applicable to that goal?
Beyond your development as a LA, we are also interested in your development as a student and as a person. To what extent have the topics discussed in this course been useful beyond your LA experience?
Reflect on your teaching interactions now as compared to the start of the term, including the "specific commitment" you made early on. What have you gotten better at this term?
How has the experience of being a LA impacted you as a student? Do you find yourself thinking/acting differently (in class, when studying, when discussing or working with peers, or in other areas of life) in ways that you think have been influenced by your LA experience? Explain/describe.
 Projects
Projects
Below are multiple suggestions for term projects for LAs. We suggest one project per term.
General instructions
The task for this project is to interview a single person to learn about their ideas about a physics concept. Your only purpose in this interview is to learn about their idea. Your purpose is NOT to teach them anything.
- DO: Openly inquire into their thinking, with curiosity. Ask questions for the sake of finding out. Paraphrase what you understand them to be saying to see if you are understanding them correctly. Spend at least 30 minutes learning about their idea.
- DO NOT: Teach, lead, coax, help, critique, challenge, correct, give feedback, judge, or in any way attempt to change, repair, or fix your interviewee's ideas.
Assignment 1: Interview topic
- Choose one of the posted physics problems (below) to use for your interview.
- Write your own answer to the question/problem, using your best conceptual physics understanding.
- Write some questions that you want to ask your interviewee along the way, to help you learn about their thinking. Some prompts you might consider: “what do you mean?” “tell me more about that.” or “can you walk me through your thought process about ____?”
Physics problems to choose from:
- Are all the colors in the rainbow?
- Is the burn one may get from touching a hot pan the same as, or different from, a sunburn?
- If you were trying to throw a ball as far as you could, would you be more successful throwing the ball on Earth or on the moon?
- A bird is temporarily contained in a large sealed glass container (with plenty of air), which is placed on a scale. When the bird flies in the container, does the reading on the scale change?
- A monkey hangs on a rope. The rope goes up over a pulley, and on the other end is a weight, which exactly balances the monkey. Everything is initially stationary. Then, the monkey tries to climb the rope. What happens?
Assignment 2: Interview subject
- Describe the specific person that you will be interviewing. This person should have agreed to be interviewed by you. Don't tell us their name (for confidentiality), but do tell us generally who they are, how you know them, what their physics experience is, etc.
- State the time when you have agreed to conduct the interview (before [date]).
Assignment 3: Interview
Conduct your interview and video- or audio- record it. Post either a video of your entire 30-minute interview, or the entire transcript of your interview. You can use Zoom’s AI transcription for this, or an AI transcription service like otter.ai.
Assignment 4: Episode transcript
- Choose a short episode (1-5 minutes) from your interview that (1) shows part of your interviewee's physics ideas and (2) is interesting to you.
- Transcribe at least one minute and no more than five minutes. If you use an automatic transcription service, check the accuracy of the transcript.
- Use a pseudonym for your interviewee.
- Number the lines of your transcript (to make it easier to discuss later).
Assignment 5: Reflection
Write a reflection on your experience of conducting this interview and/or the content of the interview. Address the following questions:
- What gestures, questions, representations, gave you insights into the interviewee’s thinking? What went well? What could have gone better?
- Were there instances (questions, gestures, representations, etc.) where you coaxed, helped, critiqued, challenged, corrected, (etc) your interviewee’s thinking? Describe at least one instance of this (unless you’re sure it never happened).
- What (if anything) did you learn/discover?
- What (if anything) did the person you interviewed learn/discover during the course of this interview? Point to specific moments in the interview that give evidence of this learning/discovery.
Satisfactory reflections must do the following:
- Be posted on time
- Consist of at least 500 words
- Be accurate about the interview material
- Draw explicit connections to teaching or learning experiences you have had
- Convey something that personally struck you as interesting, compelling, engaging, or otherwise moved you
- Write in a clear manner – your style can be less formal than typical academic prose, but it should be serious and engaged with ideas
- Contain no more than 3 errors to Standard Written English
Assignment 6: Presentation
In class, we’ll role-play each other’s transcripts and discuss what we notice.
This project is to analyze a video episode of yourself interacting with students, especially in terms of [theme - e.g., student ideas or group dynamics].
Assignment 1: Recording plan
Describe how you will record yourself interacting with students in class. A satisfactory recording plan will enable you to
- Record at least three different interactions with groups of students in your class, each at least 2 minutes long, and
- Capture both audio and video, so that everyone in the interaction can be seen and heard.
You may recruit fellow LAs to help. If there is anything you will want the professor to do, make that request now.
Assignment 2: Sample recording
Make a sample video recording of yourself interacting with a group of students and submit it here. A satisfactory sample recording meets these criteria:
- You are interacting with a group of students.
- You and the students you interact with can all be heard and understood.
- To the extent possible, you and the students you interact with are all visible. (Inevitably there will be the back of some people's heads.)
- The recording is at least 2 minutes long.
- You are able to either submit the recording to this Canvas assignment or transmit it to the instructor some other way. (Some recording techniques result in files that are too large to submit or send. If this is the case for you, find a way to either make your files smaller, or successfully transmit larger files.)
Assignment 3: Three recorded episodes
Record and submit three video episodes of yourself interacting with students in class.
A satisfactory episode meets the same criteria as for the sample video recording PLUS:
- It illustrates [theme - e.g., student ideas or group dynamics].
Assignment 4: Transcript
Transcribe one of the three episodes you submitted and submit the transcript here. A satisfactory transcript meets these criteria:
- Represents least two minutes of your interaction with students
- Clearly indicates who is speaking when, and what they are saying
- Describes any non-verbal interactions that seem important (gestures, eye contact, etc)
- Uses pseudonyms in place of students' names
- Is line-numbered
Assignment 5: Reflection
Write a reflection on the episode you transcribed, including responses to the following questions:
- What [theme - e.g., student ideas or group dynamics] do you notice?
- How did you respond?
- What would you do the same way if you were in this situation again?
- What would you do differently if you were in this situation again?
A satisfactory reflection:
- is at least 500 words long
- makes clear connections to course readings and/or discussions
- is accurate about the course material
- is written in standard English, though you do not need to use formal academic language or tone
- is posted on time.
Assignment 6: Presentation
In class, we’ll watch each other’s videos and discuss what we notice. [Alternative: In class, we will re-enact the episode using the transcript and discuss what we notice.]
- You will have the floor for 15 minutes.
- [Instructor] will bring enough copies of your transcript for everyone, will be ready to play your selected video episode, and will serve as timekeeper.
- Please lead an interactive discussion of your selected episode. Focus on the reflection prompts from Assignment 4, but don't just say your answers to these questions -- lead an interactive discussion, in which you invite us to share our observations and ask you questions.
Overview
At the end of this term, you will share your development with other Learning Assistants, Faculty Mentors, Pedagogy Instructors, and the campus community at large during the [name of poster session].
- The [name of poster session] will take place on [date/time] in [location].
- You are expected to attend this poster session for at least 90 minutes.
- Your poster will illustrate your individual growth and experiences as an LA, working from one of a few possible prompts or one of your choosing.
- Your poster will highlight evidence and examples to promote conversation with visitors.
- In addition to sharing your experiences, you will give feedback to other LAs about their presentations by visiting their posters and engaging in conversation.
Developing your poster
How have you developed as an LA and student throughout your LA experience? How has your development been related to your specific class? Track your own development from the beginning to the end of your time as a LA by examining how you understood and implemented concepts discussed in your pedagogy class and prep sessions. This is your opportunity to demonstrate your learning in this class, and also, the aspects of your role and development as an LA that you are excited to share with others! What have you learned as a LA that’s worth sharing with the rest of the LA community?
Each poster presentation should answer one of the following prompts:
- YOUR GROWTH. What did you learn as a LA? Describe your growth throughout your LA experience. Many of you came in with previous experiences in tutoring or teaching--what did you learn that built upon these formative experiences? What evidence do you have to demonstrate your growth? What structures, lessons, and/or interactions helped you grow and change in these regards?
- YOUR IMPACT ON STUDENT LEARNING. How did you impact student learning? What evidence do you have to support these claims? We expect you to be able to fluidly discuss specific actions you have taken and how these aligned with skills and overarching concepts of pedagogy discussed in your LA training. How did the ways you supported student learning evolve throughout your experience? What structures, lessons, and/or interactions helped you develop your approaches to supporting student learning?
- YOUR RECOMMENDATIONS. What advice do you have for future LAs and/or faculty for your specific course? What is it about the subject area and specific ways in which you interacted with students that led you to use certain pedagogical techniques? Which skills are most important for LAs in your specific context? What evidence do you have to support the importance of these particular techniques? What kinds of opportunities could you imagine LAs in your position engaging in during future courses that would promote better student learning and LA-student interactions? How can LAs be better utilized to promote student learning in this class? Recommend small or large changes.
- YOUR CHOICE... Propose a topic of your choosing to your instructor for approval as a final project.
Assignment 1: Examine examples
These examples show the type of content we expect: [examples here]
- Choose 3 of these that appeal to you.
- For each one, write at least 100 words saying what you learned from it and what qualities of this example you want to emulate.
Assignment 2: Choose prompt and plan evidence
- Commit to one of the four options described above.
- Describe the evidence you will need to support your presentation.
- Describe how and when you will gather the above evidence.
(To help you follow through on this commitment, your instructor will create specialized assignment(s) for you in the coming weeks: e.g., if you’re going to administer a survey, she will create assignments for you to (1) create and (2) administer the survey.)
Assignment 3: Present evidence
By now, you have gathered evidence to support your poster presentation. Analyze this evidence and share it visually. If your evidence includes quantitative data, use data visualizations (bar charts, pie charts, etc) to show patterns and trends in the data you collected. If not, think about how you will visually show what you’ve found.
Assignment 4: Main finding
- Watch this video about better scientific posters: How to Create a Better Research Poster in Less Time
- Draft the main finding – the single sentence that will be in giant letters in the middle of the poster. We will workshop everyone’s sentences in class.
Assignment 5: Draft poster
Submit a draft of your poster presentation here. In class, we will display and discuss each draft, to give you feedback before you prepare your final presentation.
Assignment 6: Verbal presentation (in class)
Presenting your poster at a poster session actually means having conversations, not delivering a speech. In class, we will each practice the opening line of our poster conversation.
Finally: Present at poster session.
Meet one or two other LAs at other universities and teach us about them. [Instructor] will provide you with contacts.
- For each LA that you meet, arrange and record a 30-minute one-on-one conversation with the other LA. Sample conversation prompts:
- "Tell me about yourself. What is your story?"
- "Please describe the LA program in your department." (size, discipline(s), application process, prerequisites, etc)
- "What are your duties as an LA?"
- "What are you good at as an LA? What are you trying to improve?"
- "What difference has being an LA made to you, if any?"
- "What difference do you think LAs make in your department, if any?
- "What advice do you have for me as a new-ish LA?"
- "What advice do you have for our new-ish program?”
- Make a creative image that represents the LA and their program. This image may NOT include either a photo of the LA or the name/logo of their school or program. You and the LA can do this together, or you can do it yourself and share it with the other person. You and they must both "sign" this work.
- During a class period of your choosing, tell us about each LA that you met and share each creative image. You are responsible for 15 minutes of class for one LA introduction, 30 minutes for two.
- Submit:
- A recording or transcript of your entire conversation
- Written answers to the conversation prompts listed above; minimum 300 words
- The creative image of the LA and their program, "signed" by both you and the other LA
Attend a virtual LA poster session hosted by another university. The assignment is to re-present three of the posters you see to us in the class.
During the poster session: Get the information you need and document your experience so as to complete the tasks below.
During a class period of your choosing: Spend at least 5 minutes of class time teaching us about each poster of your choice (at least 15 minutes total).
Submit:
- A 150-word summary of each poster (x3)
- A screen shot of the most important image on each poster, with an informative caption (x3)
- A 50-word bio of each presenter, including information such as their name, school, year, major, interests, career objectives, hobbies/talents, etc. (x3)
 Peer observation
Peer observation
We recommend that all LAs engage in peer observation 1-3 times per year. The following structure may support your LAs in engaging in productive peer observation.
Assignment 1: Plan observations
- Identify two other LAs to be your observation partners.
- You will observe each of your partners interacting with students, and they will observe you.
- These may be other LAs in your class, or you may arrange to attend each other's classes.
- Ask each of your observation partners if there is anything they specifically want feedback on.
- Get their contact information.
- Plan exactly when and where you will observe each other.
- Make sure you know what room each class is in.
- Try for week [X] so that the observation is fresh when you discuss it in class during Week [Y].
- Note that your writeup of the Observation Questions will be due in Week [Y].
Assignment 2: Conduct observations
During the observation, the observer should complete an Observation Log that identifies the observed LA’s teaching behaviors and the effects on the students. This log should be a rather complete transcript of actions, interactions, and discussions during the instruction. Personal notes, comments, and reflections could be included as well. The format used should be similar to the following:
|
What the LA did |
What the students did |
Personal comments |
|
|
Assignment 3: Written responses to observation questions
After observing another LA, use the Observation Log to answer the Observation Questions. Your responses will guide your debriefing session with the LA you observed. Submit your written responses here.
Observation Questions
- What specific actions or questions did the LA use that increased student involvement, attention, participation, and thinking?
- What specific questions or actions did the LA use that elicited or clarified student ideas?
- What were some specific ways that the LA responded to student questions, statements, or answers?
- What did the LA do well during the teaching session?
- What suggestions do you have for the LA for improvement?
- Anything else that you specifically want feedback on.
Assignment 4: In-class observation debriefing
During class, the LA pairs who observed each other will engage in a dialogue. The sequence is as follows:
- The observer reminds the “observee” what they observed.
- The observee answers the Observation Questions (i.e., they reflect on their own instruction).
- The observer answers the Observation Questions.
- The pair discusses the similarities and differences between their answers to the Observation Questions.
- The dialog continues with the roles reversed.
The intent is to have the LA who was observed reflect accurately on the teaching session and identify aspects that were very effective in promoting student learning, as well as to see areas that may need work and how to address those areas.
Momentum
Conceptual starting point:
Our research team has found that students commonly use the following productive, but incomplete, ideas (or “conceptual resources”) to answer questions in this tutorial:
- Momentum is conserved and/or transferred.
- Momentum is directional.
- The kind of collision (e.g., elastic or inelastic) matters.
- Forces cause objects to speed up or slow down.
The Momentum Tutorial takes these ideas (conceptual resources) as a starting point and supports students to articulate, connect, and refine them to develop a strong model for conservation of momentum in collisions, just like scientists do.
Learning goals:
Students will be able to:
- generate rules (about changes in momentum) based on experimental observations, and apply those rules to predict/explain the behavior (relative speed and direction) of (colliding) objects.
- choose an experiment to test a rule (about changes in momentum). They may generate the experiment themselves or select it from an instructor-provided list.
- explain and predict relative speed and direction of colliding objects in terms of conservation of momentum.
- Students will be able to explain changes in momentum in terms of forces and Newton’s second and third laws: e.g., for specific collisions, “forces transfer momentum” or “the change in momentum is equal to the impulse.”
Preview Momentum Materials
Research related to ACORN Physics Tutorials on Momentum
- B. Hansen, L. Bauman, Y. Abraham, M. Valentin, and A. Robertson, Identifying student resources for understanding linear momentum, presented at the Physics Education Research Conference 2021, Virtual Conference, 2021.
What are ACORN Physics Tutorials?
- Designed to support learning environments that Attend to Conceptual Resources in Physics. Conceptual resources are “seeds of science” that can grow toward sophisticated understandings with support and cultivation.
- Based on research about student thinking in introductory physics classrooms.
- Meant to support sense-making about forces, mechanical waves, circuits, linear momentum, kinematics, and heat and temperature.
- Supplemented by instructor guides, classroom video cases, and research that can inform and support implementation.
Why use ACORN Physics Tutorials?
- To enact instruction that treats students as having good ideas that can serve as the basis for instruction.
- ACORN Physics Tutorials reliably elicit specific conceptual resources among students in our instructional contexts.
- We support you in noticing student resources as they come up and deciding what you might do next.
- To help your students engage in the disciplinary practice of sense-making about science, as they develop conceptual understandings of forces, mechanical waves, circuits, linear momentum, kinematics, and heat and temperature.
Topics
What's Included
- Worksheets for use in your classes
- Instructor guides
- Classroom video cases
- Materials for a pedagogy course for TAs and LAs
About ACORN Physics Tutorials
This project began with the observation that though there is an abundance of topic-specific research on common misconceptions and misunderstandings in physics, there was very little systematic, topic-specific, patterns-oriented research on student conceptual resources for understanding physics. We not only had questions about what those resources would be, but also whether we would learn something new, whether time-tested methods for characterizing ideas would suit a resources-oriented analysis, and whether and how curriculum developed on the basis of our findings would be effective. Ultimately, we wanted to build a pragmatic toolset for instructors who wanted to implement resources-oriented instruction but needed evidence, ideas of where to start, and course materials to work with. We think we’ve done that – at least we’ve started to – and we’ve learned a lot, some unexpected, along the way.
Learn more about resources-oriented instruction in our American Journal of Physics paper:
- A. D. Robertson, L. C. Bauman, Y. M. Abraham, B. Hansen, H. Tran, and L. M. Goodhew, “Resources-oriented instruction: What does it mean, and what might it look like?” American Journal of Physics 90, 529, DOI: https://doi.org/10.1119/10.0009796 (2022).
Have questions about ACORN Physics Tutorials? Contact Amy Robertson: robertsona2 at spu dot edu
Conceptual Questions
Introduction
We understand that not every instructor will be in a position to adopt a full-length tutorial for use in their courses. This page offers a series of conceptual questions that we have asked, analyzed, and trust to elicit a variety of resources that we consider interesting and relevant to many introductory physics learning objectives. These questions could be used as discussion questions in an introductory physics course, or as homework or quiz questions. Many of these questions are featured in ACORN Physics Tutorials, but some are not and could be used in conjunction with the Tutorials to further advance resources-oriented instruction. For each question, we include a downloadable (and editable) PowerPoint slide with the question, our answer to the question, a few sample student responses, and an overview of some of the resources we observe students using and how we perceive these resources to be connected to introductory physics learning goals.
Linear momentum
Ball/clay predict question
The ball/clay predict question tells students to suppose they want to close a door quickly but cannot reach it. The question then asks whether they would choose to throw a rubber bouncy ball or an equally massive piece of clay at the door to accomplish this task.
Our own answer to this question is that the ball will move more quickly if we choose to throw the rubber bouncy ball. With the door initially at rest, the initial momentum of the system is the momentum of the clay/ball. If we assume these initial momenta are the same (e.g., we throw them with the same speed in the same direction and they are equally massive), then the vector
representing the momentum of the system points in the same direction and is the same length for both scenarios. The clay sticks to the door and continues to have a component of motion in its original direction, and the rubber ball bounces and moves in the opposite direction. By vector addition, the final momentum of the door (which moves in the ball’s original direction of motion) would be higher with the rubber ball.
The ball/clay predict question is a predict-style question, a type of question that asks students to apply principles and ideas to a new scenario. Students used a variety of resources in their responses to this question, ranging from applying rules and constraints they may have learned in physics class (using terms like “isolated system,” “momentum conservation,” and “elastic and inelastic collisions”), to sense-making about what an inelastic or elastic collision is (drawing on ideas of force and energy). For example, one student wrote:
“The momentum when it approaches the door is positive. Assuming this happens in a closed system, momentum is conserved. So, when the bouncy ball hits the door, it moves in a negative direction & has a negative momentum, causing the door to have a positive momentum in the opposite direction.”
This (correct) written student response illustrates attention to both the conservation and the directionality of momentum at different moments during and after the collision.
Another student wrote:
“The [motion of the door will be the] same. When they [rubber ball and clay] collide the door, the momentums of the door change in the same magnitude because they have the same mass.”
This student reasons that since the rubber ball and clay are equally massive, the door they hit will experience equal changes in the magnitudes of momentum. While this response is canonically incorrect, the student is both (i) considering a property of the objects (mass) that are relevant to momentum and (ii) recognizing that the properties of the object matter for what happens in a collision between them. Many students used similarly structured arguments, reasoning that because the objects that collided have a certain property (hard, soft, bouncy, heavy, light, fast, etc.), their momentum changes in a certain way.
Some students provided a mechanism that explained why they thought either the rubber ball or the clay would shut the door more quickly. For example:
“I would throw the piece of clay at the door because it wouldn’t bounce off as much. More momentum would be transferred from the clay.”
This student (and others like them) reasoned that because the clay stuck to the door, it transfers more of its momentum to the door. Other students answered that the bouncy ball has more oomph and so transfers more of its momentum to the door, or that bouncy objects can change their momentum more.
In short, the ball/clay predict question appears to elicit resources for conservation, directionality, and identifying the kind of collision at play, as well as mechanisms that students use to explain why one collision or the other might transfer more energy or momentum.
Desk chair momentum predict question
The desk chair momentum predict question tells students that two people are facing one another in desk chairs with low-friction bearings and that one of the people tosses a large, heavy ball to the other. They are asked whether the student who tosses the ball will remain at rest, and whether the student who catches the ball will remain at rest.
This predict-style question is similar (but not identical) to questions found on the Energy and Momentum Conceptual Survey and the Force and Motion Conceptual Survey. Our answer to the desk chair momentum predict question is that the student who tosses the ball will begin moving opposite the direction they toss the ball, and the person who catches the ball will begin moving in the direction of motion of the ball as they catch it. We can make sense of the catcher’s movement in terms of momentum transfer: when the ball collides with the person, it gives some of its momentum to the person, and they begin to move. The ball and the person move more slowly than the ball did originally because of momentum conservation: when the ball gives some momentum to the person, it moves slower. The person is presumably more massive than the ball and receives only a part of the ball’s momentum so also moves slower than the ball did. For the thrower: the original (vector) momentum of the system was zero. When the ball moves one way, the thrower must move the other way to conserve momentum.
The desk chair predict question elicited a variety of resources, often relating to momentum conservation and transfer. Some of these resources resembled rules or procedures: momentum is conserved, momentum can transfer, analysis of systems, or efforts to “balance” or “equalize” momentum (connected to, but not precisely, momentum conservation). Others resembled mechanisms for momentum transfer (e.g., forces). For example:
“No. They will both move farther apart. For the first, momentum one way leads to momentum the other way. Second, the momentum of [the] ball transfers to the person.”
This response uses a sort of “momentum balancing,” reminiscent of (and a resource for) momentum conservation, to determine that the thrower will move opposite the direction of motion of the tossed ball. They use momentum transfer (which implies conservation) to decide that the catcher will also move.
Another student responded:
“If you break the situation into two different systems: the thrower and the catcher, the thrower system is elastic and the catcher system is inelastic. This helps us because when looking at the thrower system, the thrower is initially at rest but then when throwing the ball we know that momentum needs to be conserved so the student will move backwards canceling out the motion of the ball. Then when the other student catches both the student and ball ‘stick’ together and move in the same direction.”
This response draws on a variety of resources, including identifying systems, to conclude that both the thrower and the catcher will move. They name two relevant systems for this scenario – (1) the thrower and the ball and (2) the catcher and the ball – and identify one collision as elastic and the other as inelastic. Though it’s not totally what this student means by “elastic” and “inelastic,” they are drawing on resources for identifying systems and types of collisions that connect with learning objectives in introductory physics in ways that instructors might build on.
Some students drew on Newton’s third law to make sense of the direction of motion of the thrower and the catcher. For example:
“No - neither remains at rest. Both catching and throwing the ball requires a force and these forces come in equal/opposite pairs, so applying a force to move the ball/slow it down will also apply a force to you in the chair that moves you.”
Here, the student argues that as the thrower applies a force to move the ball, the ball exerts an equal and opposite force on the person, such that the person will move (accelerate) in the direction opposite the ball’s motion. Likewise, when the catcher applies a force opposite the ball’s motion to slow it down upon catching it, the ball applies an equal and opposite force to the catcher, accelerating the catcher in the direction of the ball’s motion.
In summary, the desk chair momentum predict question appears to elicit resources for momentum conservation and transfer, as well as resources that connect forces and energy to momentum, all goals of introductory physics instruction in the context of linear momentum. The desk chair momentum explain question (PowerPoint slide) is an explain-style question that elicits similar resources.
Circuits
Rank the bulbs explain question
The rank the bulbs explain question shows students a circuit with four bulbs (see PowerPoint slide) and a switch, and ranks the brightness of the bulbs when the switch is closed (part a) and then opened (part b). Students are asked to say why the rankings are observed.
This question is featured in our ACORN Physics circuits tutorial, and in using it there and elsewhere, we sometimes find that it can help to break question (b) into several parts, highlighting the dimming of bulbs B and C, the brightening of bulb A, and bulb D going out altogether separately. This is an explain-style question that describes a phenomenon and asks students to sense-make about it, rather than to predict a particular outcome. It was adapted from [cite McDermott and Shaffer paper]. Our own answer to this question relies on current tracing and Ohm’s Law: in the original (closed switch) circuit, all of the current from the battery goes through bulb A, then splits equally through bulbs B and C (which are identical), then recombines to go through bulb D. This makes B and C equally bright but dimmer than A and D, which are themselves equally bright (since the current is conserved as it splits and recombines). When the switch is opened, the branch with bulb C is no longer complete, and what was originally a two-bulb parallel circuit element becomes a single-bulb series element, such that the circuit is effectively a three-bulb series circuit. This increases the resistance, decreasing the current through the battery. Thus bulbs A and D, which originally received all of the current from the battery, dim. Bulb B, now in series with the battery, brightens, and bulb C does not light.
Students used a variety of resources for understanding current, voltage, and resistance to answer this question. Most commonly, students focused on current as responsive to changes in the circuit (including different connections) and resistance as limiting current. For example:
“...when the switch opens, bulb B joins the series instead of just being in parallel to bulb C, so resistance increases. The battery is the same so V remains the same. Therefore current must decrease to compensate.”
This response acknowledges that the way the circuit elements are connected matters for the properties (in particular, the resistance) of the circuit, naming that the resistance increases if you take away a parallel branch. The student draws on the resource that current is responsive to changes in the circuit; when voltage remains the same but resistance increases, “current must decrease to compensate.”
Another student wrote:
“When the switch is opened, the current no longer has the option to split and flow through either B or C, it must all flow through B. Since B and C are no longer in parallel, the overall resistance of the circuit is greater than when the switch is closed. With greater resistance, there is less current according to Ohm’s Law. And since the luminosity of a light bulb is directly proportional to current, this means dimmer light bulbs as well.”
Here, the student uses current tracing (conservation of current) to analyze how changing the connections in the circuit will change how the current moves through. Like the previous response, this student acknowledges that removing a parallel branch increases the resistance of the circuit, which increases the current by Ohm’s Law.
As might be expected with complex circuits that contain many elements, students’ analyses in the rank the bulbs explain question include multiple parts that include a variety of resources. We are especially interested in the ways in which these responses articulate a nascent conceptual model of current as responsive to changes in the circuit (including changes in resistance and changes in how elements are connected to one another), a resource that appears to be consistently activated in this context.
Order of elements explain question
The order of elements explain question is an explain-style question that shows students two circuits, both of which have three batteries and three bulbs in series, with all of the batteries facing the same direction. However, in the second circuit, rather than having three bulbs then three batteries in a row, the elements are arranged bulb-battery-bulb-battery-bulb-battery. Students are told that all six of the bulbs in the two circuits are equally bright and are asked why this is the case.
As with the rank the bulbs explain question, students drew on resources that highlighted that current is responsive, this time also foregrounding that voltage drives current, alongside attending to resistance as opposing current and the connections between elements as relevant. For example:
“[...] In circuit A, the batteries are all in a row which increases the total current but the resistors are also in a row which would decrease the total current. Circuit A has 3 times the voltage but also 3 times the resistance, which would result in the same current. Circuit B also has the same current because the voltage is one and the resistance is 1, but it happens three times in series.”
Though it isn’t clear to us how this student calculated the voltage and resistance (as 1 for Circuit B, and as “three times” for Circuit A), it is clear that they are framing voltage as driving current, resistance as limiting it, and current as responsive to both. It may be that they think of the current as going up and then down (changing as it moves through the circuit); whether or not this is the case, we can identify resources in this response that we could leverage to support conceptual understanding of voltage, current, and resistance.
Similar notions of voltage as driving current and resistance as limiting it are observed in this student response:
“[It] makes sense [that all the bulbs are the same brightness] because the current is the same everywhere in the wire and is being pushed forward by the same amount of voltage from the batteries and resisted by the same amount of resistance.”
This student justifies not only that the current should be the same in the two circuits, but also that the current should be the same throughout each circuit, using language of “pushed” (for voltage) and “resisted” (for resistance).
Some students focused on the two circuits having similar types of connections (rather than, say the same numbers and types of elements). For example:
“[...] Since electrons flow as a stream through the wire, the positioning of the components doesn’t matter in this case. The “stream” is being slowed down by the bulbs, and pushed by the batteries, doesn’t matter where. In tug of war for example, it doesn’t matter much where you position the people pulling, as long as they are somewhere on the rope.”
Here the student models electrons as a stream flowing through the wire, extending that model to then say that the positioning of the elements doesn’t matter. They advance this model by saying that the effect of the elements is to push, in the case of batteries, and slow things down, in the case of resistors, and it doesn’t matter where in the “stream” (or the rope, in their tug-of-war analogy) this happens; it just matter that it does.
Both the rank the bulbs explain question and the order of elements explain question provide contexts for eliciting a conceptual model for current as responsive to elements and their order, resistance as limiting current, and voltage as driving current. The order of elements question appears to foreground voltage-as-driver more than the rank the bulbs question, which appears to more frequently cue the resistance-as-limiting resource, at least for the samples of student responses we analyzed.
Mechanical waves
Tension pulse flick question
The tension pulse flick question gives students two scenarios: one in which a TA creates a pulse by flicking a spring attached to a wall, and the second in which the same TA pulls the spring taut and flicks the spring in the same way, creating a second pulse that propagates down the spring more quickly. The question asks students why it would make sense for a pulse to move faster on a higher-tension spring.
The tension pulse flick question is an explain-style question that provides a description of an observation and asks students to say why it makes sense (or doesn’t) to them. The question is a revised version of a question on the Waves Diagnostic Test. Our answer to the tension pulse flick question is that as the spring becomes more taut, the (tension) forces between adjacent parts of the spring increase, such that when one part of the spring is displaced by the disturbance, it pulls the adjacent parts more, and the pulse is propagated down the spring more quickly.
Student responses to the tension pulse flick question drew on resources that highlighted the ways in which the properties of the medium affect the motion of the pulse, that focused on the up-and-down motion of the spring as the way in which the pulse propagates (and how this motion is affected by changes to the properties of the spring), and that brought in ideas about forces and energy to explain changes in the speed of the pulse. For example:
“The higher the tension of the spring, the more sensitive it is to movement so the pulse can travel faster.”
This student explains that the speed of a pulse depends on the tension in the medium because increased tension means the medium can react more quickly to the pulse. The student goes beyond naming the relationship between tension and pulse speed, toward a nascent causal association.
Other students focused on the forces between parts of the spring, as we did in our answer to the tension pulse flick question. For example:
“When the tension is higher, the particles (or small part[s]) of the springs are pulling each other with more forces. If one particle goes upward, then the particle next to it will be dragged upward. With more forces (= higher tension), it gets dragged even faster (tightly bound). This speed of getting dragged is the speed of the wave, so the higher the tension [the] higher the speed. (c = T/, with same μ.)”
In focusing on a “point,” a “particle,” or a “part” of the spring, this response implies a discretized model of the medium. The student argues that increasing tension makes each particle accelerate more quickly, increasing the wave speed, drawing on reasoning about forces to make sense of pulse propagation.
Students sometimes used reasoning about energy to make sense of faster pulses on higher-tension springs. For example:
“Having a tighter string means less energy gets represented as vertical displacement so that more energy goes into the pulse’s forward movement, i.e., speed.”
In this example, as in many sample textbook solutions that encourage students to break up the energy of a system into its varied forms, the student reasons that in pulse propagation, some energy is in the form of vertical displacement and some in the form of forward movement. When the tension is increased, they reason, the pulse does not go as high, so more energy is able to be “put into” forward movement. Though incorrect, this response associates energy with the shape (“vertical displacement”) of the spring, and associates the speed of the pulse with the tension in the medium, reasoning that energy is associated with or carried by the pulse itself and that energy transfers and transformations play a role in the speed or motion of the pulse.
In general, our experience is that the tension pulse flick question elicits ideas that support student thinking about how propagation happens and why the medium and its properties matter, often drawing on mechanics concepts like force and energy in sense-making.
Mass density pulse flick question
The mass density pulse flick question is very similar to the tension pulse flick question, except the property that is changed between the first and second scenario is the mass density–not the tension–of the spring. In particular, the TA replaces the first spring with a second one that has a higher mass density, and observes that the second pulse moves more slowly down the spring. Students are asked why it would make sense for a pulse to move more slowly down a spring with higher mass density.
The mass density pulse flick question, like the tension pulse flick question, is an explain-style question. Our answer to this question is again based on a model in which a pulse propagates by pulling on adjacent parts of the spring. If the tension (and thus the forces between parts) of two springs is the same, but the mass of the parts of one spring is more than the other, the accelerations of the pieces of the more massive spring will be smaller, and the pulse will propagate more slowly.
As with the tension pulse flick question, student responses to the mass density pulse flick question drew on resources that highlighted the ways in which the properties of the medium affect the motion of the pulse, that focused on the up-and-down motion of the spring as the way in which the pulse propagates (and how this motion is affected by changes to the properties of the spring), and that brought in ideas about forces and energy to explain changes in the speed of the pulse. For example:
“Springs have inertia and heavier springs will have more inertia because inertia is proportional to mass. Since inertia is the tendency to resist change in motion, a heavier spring will oppose the motion of a pulse more.”
This example draws on ideas from mechanics–particularly inertia or a “tendency to resist change in motion”–to make sense of why the speed of the pulse would decrease as the mass density increases.
As in the tension pulse flick question, some students analyzed the spring as a series of discrete chunks, and sense-made about how an increase in mass density would affect the interactions between chunks. For example:
“It would make sense for the pulse to move more slowly on a heavier spring because you could represent each point of mass on the string with a free body diagram and the Fnet on each point of mass is equal to mass times acceleration. (Fnet = ma) Therefore, if the Fnet on each spring is the same as scenario 1, when the mass increases in scenario 2, the acceleration must decrease to compensate. This means that each point on the spring will accelerate more slowly when moving away from the ‘center line’ of the spring, effectively resulting in the pulse moving more slowly.”
This student response closely resembles the answer we offered, adding a reference to the displacement from the spring’s equilibrium.
Also similar to the tension pulse flick question, a number of students performed an energy analysis, splitting the energy among types of movements and reasoning about how changing the mass would affect this split. For example:
“In a heavier spring, there is more mass in a given unit of length. It would take more energy to displace this mass than in a lighter spring. Since more energy is spent on actually displacing the spring in a wave there will be less energy to drive the pulse’s velocity, given that the same amount of energy was applied each time.”
Here, the student reasons that it would take more energy to move a higher-mass chunk (“a given unit of length”). This would leave less energy to “drive the pulse’s” forward movement, and therefore the pulse would propagate more slowly. Though not necessarily canonically correct, this response productively associates energy with the dynamics of pulse propagation.
In our experience, both the tension and mass density pulse flick questions offer an opportunity for students to go beyond understanding that propagation speed is the square root of tension divided by mass density, toward reasoning about how the properties of the medium affect the speed of the pulse. In many cases this reasoning includes modeling the medium as a discrete series of chunks that interact with one another, modeling the pulse as a disturbance that moves these chunks up and down, and drawing on the concepts of forces and energy to explain the dynamics of pulse propagation.
Fixed end reflection question
The fixed end reflection question tells students that pulses reflect on the opposite side of the spring at fixed ends, and then asks them why they think that happens.
This is an explain-style question. In answering the fixed end reflection question ourselves, at a level that is appropriate for introductory physics students, we analyze the forces on the spring at the fixed end. As the pulse reaches the fixed end, the spring pulls up on the wall, and Newton’s third law tells us that the wall pulls back on the spring, exerting a force downward on the segment of spring that is adjacent to the wall. The downward force from the wall is greater than the upward force from the segment of spring on the other side, the segment closest to the wall accelerates downward and overshoots equilibrium to the other side.
As we anticipated, students often used the concepts of forces and energy to explain the behavior of pulses at fixed ends, constructing responses with varying degrees of mechanism. For example, one student wrote:
“Every action has an equal and opposite reaction. So as the wave propagates towards the wall, and hits the wall, there is a force upwards on the wall. This means the wall exerts a force downwards on the string. Because F = m(dv/dt) and the wall does not accelerate, the string accelerates downwards, effectively inverting the wave. Also, maybe something to do with energy, ID[on’t]K[now].”
This response applies Newton’s second and third laws to the part of the string near the boundary (the wall), arguing that the pulse is inverted because the string pulls up on the boundary, and the boundary pulls down with an equal and opposite force, which causes the string to accelerate and move past the equilibrium point.
Other students applied energy concepts to reason about reflection on the opposite side of a spring at a fixed end. For example:
“… I believe that the reason it reflects to the other side is due to conservation of energy. Because the wave constantly wants to displace upwards, however [it is] unable to b/c of [the] fixed end. The only way it can go to maintain its energy is to deflect downward. Furthermore, energy has no direction, nor does it care about direction, therefore reflecting downwards does not change the energy state.”
Here, the student argues that conservation of energy requires that a pulse continue (it can’t just disappear), and since it can’t keep going up at the fixed end, it has to “deflect downward.” They add that because energy doesn’t have a directionality (only a magnitude), the top and bottom of the spring are effectively the same.
Some responses to the fixed end reflection question used procedures–such as modeling the reflected pulse as the superposition of the “incoming” pulse and an inverted “ghost” pulse–but this was less common than responses that drew on concepts of forces, motion, and energy to explain why the reflected pulse was on the opposite side of the spring. This suggests to us that the fixed end reflection question may support students in bridging ideas from mechanics to sensemake about fundamental pulse reflection phenomena.
Superposition mechanism question
Like the tension pulse flick question, the mass density pulse flick question, and the fixed end reflection question, the superposition mechanism question is an explain-style question that describes a fundamental wave mechanics scenario and asks students why they think it happens that way. In particular, the superposition mechanism question tells students that when two pulses on the same side of a spring meet, they add–an example of superposition. They are then asked why pulses add when they are on the same side of the spring, or why superposition works the way it does.
Our hope was that students would go beyond restating the principle of superposition (mathematically or conceptually) and instead draw on mechanics principles to sensemake about the phenomenon. Our answer to the superposition mechanism question is that the leading edge of each pulse pulls upward on the segment of spring between them just before they meet. The force by each leading edge on this “middle segment” is determined by the tension in the spring and the shape of each pulse (sharper pulse means higher force). This means the “middle segment” accelerates in a way that is determined by the sum of the forces delivered by each leading edge. This kind of logic can be extended to the entire time period that the pulses overlap, leading to the same conclusions that the mathematical principle of superposition does.
As we had hoped, students did draw on mechanics concepts–particularly forces, energy, speed, and acceleration–to explain why pulses add when they are on the same side of the spring.
“If the strings are both accelerating up, they will both accelerate up with twice the force.”
This response makes sense of superposition using the acceleration of parts of the spring. When two pulses that are both accelerating the spring up superpose, the string then “accelerate[s] up with twice the force,” making the string move even higher.
Another student responded using imagery of free body diagrams, writing:
“Imagine that the two pulses are forces acting upon an object in the same direction. [Drawing of box with two arrows whose tails are on the right side of the box and heads are pointing horizontally outward from there.] The total force on the object would be the sum of these two forces (constructive interference).”
Here, the student analogizes constructive interference to a sum of forces, where the spring is the object and the pulses are forces. When the forces are in the same direction, the spring experiences a net force that is the sum of those two forces, displacing it further.
Yet other students used energy to sensemake about superposition. For example, one student wrote:
“This principle is in line with the conservation of energy, if they weren’t added together, energy in the wave would be lost.”
While this response isn’t as clearly mechanistic (to us) as responses that draw on acceleration and forces, it does associate energy with the amplitude of the pulse, and uses conservation rules to sensemake about why the pulses can’t just disappear.
Some students also drew on resources for reasoning about what a pulse is, arguing that pulses superpose because they can occupy the same space at the same time (in contrast to, say, discrete objects).
“Superposition works because waves can occupy the same space at a given time therefore the net wave is the sum of the waves. Since the waves are on the same side, their displacements are (in this case) ‘positive’ and we add the pulses.”
These responses are less obviously about what makes pulses add when they are on the same side of the spring and are more clearly about what it is about pulses that makes it possible for them to add in the first place. This ontological characterization of pulses as not-objects challenges some of the findings from misconceptions-oriented studies of student understandings of waves, suggesting that the extent to which students think of pulses as objects depends on the context.
In short, the superposition mechanism question, like the other waves questions we’ve offered here, may be especially appropriate for supporting connections between mechanics ideas and wave dynamics, and (in this case) for eliciting ideas about the nature of pulses as displacements of the spring that can co-occupy space.
Heat and temperature
Metal blocks question
The metal blocks question tells students that two metal blocks sitting on a table, one hot and one cold, are placed in contact with one another, and that over the next several minutes, the blocks become the same temperature as one another, and eventually the same temperature as the room. The question asks students what mental model helps them explain why this happens.
The metal blocks question is an explain-style question that asks students to apply a model to explain why we observe the behavior described in the question. Our own answer to this question is temperature changes happen when thermal energy moves into or out of an object. When two objects at different temperatures come into contact (such as the two blocks, one hot and one cold, or the hot block and the room), thermal energy transfers until the two objects are the same temperature. (This equilibrium-seeking could be explained in terms of entropy, micro- and macrostates, collisions between particles at the surface of the object, etc.)
Students used a variety of resources in their responses to this question, including highlighting that temperature changes as a result of thermal energy transfer, naming properties that affect temperature change or thermal energy transfer (e.g., temperature difference, mass or material of objects), citing the Second Law of Thermodynamics, identifying collisions between particles as a mechanism for energy transfer, and evoking a model of a reservoir to explain undetectable changes in temperature (such as in the environment).
For example, one student wrote:
“Heat flows from hot environments to colder environments. So I would think as soon as the cold block touched the hot block heat was transferred to it, and heat from the hot block was being released to the environment via heat waves. So as the heat that is being transferred into the cold block, as soon as the heat enters the cold block it is also emitted into the environment.”
This response draws on a number of resources for understanding thermal phenomena, including the Second Law of Thermodynamics, the idea that thermal energy transfers at contact, and the awareness that multiple objects at different temperature are in contact.
Some students articulated a mechanism for thermal energy transfer at contact. For example:
“There is a transfer of kinetic energy between fast moving molecules (in the hot block) with slow moving molecules (in the cold block). Which facilitates the transfer of having both blocks being the same temperature.”
Here, the student articulates that particles in the hot block will be moving faster than particles in the cold block, such that when the two come into contact, energy will transfer between them.
Students also referenced diffusion and reservoirs, for example:
“The concept of diffusion, hot air will travel to the cold and cold to hot until it reaches equilibrium. The heat in both block will reach back and forth but the room is way bigger, the heat from both block will expand towards the room, but the size of the room is way bigger, both hot and cold waves of temperature would just decrease and increase until it is at an equilibrium with the room temperature.”
This student paints an image of thermal energy exchange and movement through space, where energy travels between objects until equilibrium is reached. They justify the stable temperature of the room in terms of it being big, like a reservoir where thermal energy can spread out such that the temperature change of any one part is negligible.
In the metal blocks question, as with other thermal physics questions we asked, elicited a variety of resources, many of which blended everyday and physics classroom language to predict or explain thermal phenomena. The metal blocks question in particular appears to foreground energy transfers at contact, and equilibrium-seeking, alongside some mechanisms for both.
Heat-transfers-from-hot-to-cold question
The heat-transfers-from-hot-to-cold question cites a colloquial version of the Second Law of Thermodynamics – that heat or thermal energy transfers from hot to cold – and asks students how they make sense of this. The format of this is an explain-style question, but the content is somewhat different; rather than asking students to explain the observed behavior of a system, we ask them to say how they make sense of a “rule” they have learned in physics class.
There are a variety of canonically correct answers to this question. Our answer focuses on the microscopic processes: microscopically, hot objects have higher temperatures, which corresponds to particles with higher kinetic energy. When two objects come into contact, one hot and one cold, the interactions between the higher—and lower—energy particles at the point of contact transfer some of the energy to the colder object.
Students used a variety of resources in their responses to this question. Some responses were tautological–e.g., thermal energy transfers from hot to cold because that’s what thermal energy does–but many responses gave us insight into how students are thinking about thermal energy, equilibrium, and entropy.
Several student responses mimic our microscopic analysis. For example:
“Thermal energy is a result of the movement of the particles so there is no way you could transfer no movement, so the only direction is transferring movement to no movement.”
Though this student is incorrect in suggesting that colder objects have no particle movement at all, this response does name a mechanism for the directionality of thermal energy transfer: collisions between particles moving at different speeds.
Other student responses gave us insight about how they might be thinking about equilibrium (and thus what kinds of activities or analogies might support continued conceptual development). For example, one student wrote:
“Heat transfers from hot items to cold items because of the universe’s ‘need’ for balance. Equilibrium is the most stable state for the universe to be in and that is seen in exchange of heat as well. The hot item’s molecules have more kinetic energy than the molecules of the cold items. Energy can be shared as heat so in order for the two objects to have equal energies, heat flows from the object with higher energy to the object with lower energy.”
This response personifies the universe as having a need for balance and stability, saying that transferring energy from the hot object (whose molecules have more kinetic energy) to the cold one creates the conditions under which the two objects can have equal energies. Other responses referenced “evening out,” “concentration,” and “spreading out.”
Still other responses directly referred to entropy and micro- or macrostates, though these responses were less common. For example:
“Thermal energy transfers from hot to cold objects, and not the other way around because of entropy. Since entropy cannot decrease in a closed system, the system tends toward high entropy. One object having higher temperature than another is a more organized state than both objects being in thermal equilibrium, so thermal energy tends to transfer from hot objects to cold objects.”
This response cites a colloquial definition of entropy as being about the degree of organization of a particular state, saying that the state in which more energy resides in one object is more organized than the state in which objects share the energy equally, and thus the tendency is toward the latter.
In short, the heat-transfers-from-hot-to-cold question appears to do what it was designed to do, which is to support us (instructors and researchers) in better understanding how students are thinking about the nature of thermal energy transfer, equilibrium, and entropy.
Particles and cubes what-is-possible questions
The particles and cubes what-is-possible questions ask students what scenarios are possible as a result of given experimental set-ups. These are explain-style questions that are meant to explore student thinking about statistical probability.
The canonically correct answers to the what-is-possible questions depend on the assumptions students make. For example, if three identical cubes are left in boiling water for 5 minutes before their temperatures are measured, the final measured temperature possibilities may differ based on whether the student assumes the cubes have a small number of particles in them or a large (N ~ NA) number of particles. The second law of thermodynamics states that entropy does not decrease, which in tangible terms means that heat flows from hot to cold. For a cube system with a small number of particles, it is possible, however unlikely, for the cubes to end up with slightly different temperatures. The larger the system (or the larger the number of particles), the less likely the system is to stray from equilibrium. The 3 particle system has a higher likelihood of being “off-balance” (having particles with different speeds) than the 3-cube system (where “off-balance” would be defined as having different temperatures).
This set of questions elicited both conceptual and epistemological resources. We saw a mix of resources related to both probability and predictability. One student stated (in response to “cubes”):
“This doesn't make sense, as temperature wants to equalize, and the water would have to drain energy from one of the cubes, violating the second law of thermodynamics.”
This student demonstrates an understanding that that equilibrium is the most probable state (”temperature wants to equalize”). They also state that the outcome proposed in the question is not possible due to physics laws (”the water would have to drain energy […] violating the second law”), which we interpret as pointing to the student’s thinking about how we know in physics (epistemology).
(In response to “cubes”): “In theory, the energy in the system has the highest probability of being distributed equally to all of the cubes, thus heating them all equally. However, in practice, it is possible for more energy to enter one of the cubes than the others, thus explaining this situation.”
This student uses the resource that energy and temperature are related (”energy […] being distributed equally […] thus heating them all equally”); they also state that the stated outcome is possible, due to the random behavior of particles, but unlikely (”in theory […] highest probability of being distributed equally […] in practice, it is possible for more energy to enter one […] than the others”).
(In response to “particles”): “No, since particles collide elastically, so since all three particles initially had the same speed, they will maintain the same speed.”
This response uses multiple relevant ideas, such as the idea that identical experiments will have identical outcomes (”all three particles initially had the same speed, they will maintain”), an idea more closely tied to predictability than probability. They also draw on the resource that energy and speed are related, but particularly attend to collisions as a mechanism for energy transfer, pointing out that because the collisions are elastic, there is no transfer of energy and therefore no change in speed. (”particles collide elastically, so […] they will maintain the same speed”).
The types of ideas students used in their responses covered a wide range. More importantly, it sheds relevant light on how students think about the possibility of scenarios occurring, and the context-dependence (microscopic particles vs. macroscopic cubes) of their ideas, reasoning, and beliefs about physics.